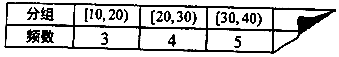题目内容
4.若tan($\frac{α}{2}$+$\frac{π}{4}$)=-2,则cosα的值为( )| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
分析 首先由两角和的正切公式求出tan$\frac{α}{2}$,然后利用余弦的倍角公式求值.
解答 解:因为tan($\frac{α}{2}$+$\frac{π}{4}$)=-2,所以$\frac{tan\frac{α}{2}+1}{1-tan\frac{α}{2}}=-2$,解得tan$\frac{α}{2}$=3,所以cosα=$\frac{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}}{co{s}^{2}\frac{α}{2}+si{n}^{2}\frac{α}{2}}$=$\frac{1-ta{n}^{2}\frac{α}{2}}{1+ta{n}^{2}\frac{α}{2}}$=$\frac{1-9}{1+9}=-\frac{4}{5}$;
故选:B.
点评 本题考查了三角函数式的化简求值;关键是熟练掌握三角函数公式.

练习册系列答案
相关题目
19.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
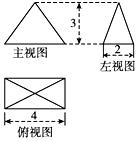

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |
9.设复数z满足z(1+i)=4,则|$\overline{z}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | 2-2i | D. | 2+2i |