题目内容
3.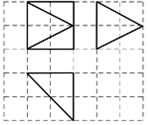 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
分析 由题意,几何意是放倒的四棱锥,根据图中数据得到关于a的方程解之.
解答  解:由题意几何体如图四棱锥P-ABCD:几何体的表面积为(2×2$+\frac{1}{2}×2×2$+$\frac{1}{2}×2×\sqrt{5}×2$+$\frac{1}{2}×2×2\sqrt{2}$)a2=$12+4(\sqrt{2}+\sqrt{5})$,解得a=$\sqrt{2}$;
解:由题意几何体如图四棱锥P-ABCD:几何体的表面积为(2×2$+\frac{1}{2}×2×2$+$\frac{1}{2}×2×\sqrt{5}×2$+$\frac{1}{2}×2×2\sqrt{2}$)a2=$12+4(\sqrt{2}+\sqrt{5})$,解得a=$\sqrt{2}$;
故选:C.
点评 本题考查了由几何体的三视图求几何体的表面积;关键是正确还原几何体.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.观察数表:
根据数表中所反映的规律,第n+1行与第m列的交叉点上的数应该是m+n.
| 1 | 2 | 3 | 4 | …第一行 |
| 2 | 3 | 4 | 5 | …第二行 |
| 3 | 4 | 5 | 6 | …第三行 |
| 4 | 5 | 6 | 7 | …第四行 |
| 第一列 | 第二列 | 第三列 | 第四列 |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )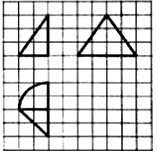

| A. | 2+π | B. | 2+4π | C. | 6+π | D. | 6+4π |