题目内容
20.在坐标平面xOy内,O为原点,点$P(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,射线OP逆时针旋转$\frac{π}{2}$,则旋转后的点P坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).分析 根据题意画出图形,结合图形,利用单位圆和三角函数,
即可求出旋转后的点P坐标.
解答 解:如图所示,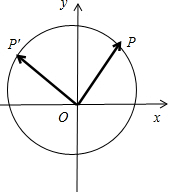
坐标平面xOy内,点$P(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,
则P(cos$\frac{π}{6}$,sin$\frac{π}{6}$);
射线OP逆时针旋转$\frac{π}{2}$,得P′(cos$\frac{2π}{3}$,sin$\frac{2π}{3}$),
即P′(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴旋转后的点P坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:$(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$.
点评 本题考查了向量旋转的应用问题,是基础题.

练习册系列答案
相关题目
11.观察数表:
根据数表中所反映的规律,第n+1行与第m列的交叉点上的数应该是m+n.
| 1 | 2 | 3 | 4 | …第一行 |
| 2 | 3 | 4 | 5 | …第二行 |
| 3 | 4 | 5 | 6 | …第三行 |
| 4 | 5 | 6 | 7 | …第四行 |
| 第一列 | 第二列 | 第三列 | 第四列 |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )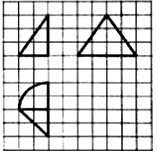

| A. | 2+π | B. | 2+4π | C. | 6+π | D. | 6+4π |
5.已知函数f(x)=6-x3,g(x)=ex-1,则这两个函数的导函数分别为( )
| A. | f′(x)=6-3x2,g′(x)=ex | B. | f′(x)=-3x2,g′(x)=ex-1 | ||
| C. | f′(x)=-3x2,g′(x)=ex | D. | f′(x)=6-3x2,g′(x)=ex-1 |
9.设复数z满足z(1+i)=4,则|$\overline{z}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | 2-2i | D. | 2+2i |