题目内容
已知a，b∈R，a≠b，且a+b=2，则（ ）
A、ab≤
| ||
B、1＜ab＜
| ||
C、ab≤1≤
| ||
D、ab＜1＜
|
考点：基本不等式
专题：不等式的解法及应用
分析：a，b∈R，a≠b，且a+b=2，可得2＞2
，2（a2+b2）＞（a+b）2，化简即可得出．
| ab |
解答：
解：∵a，b∈R，a≠b，且a+b=2，
∴2＞2
，2（a2+b2）＞（a+b）2，
化为ab＜1，a2+b2＞2，
∴ab＜1＜
，
故选：D．
∴2＞2
| ab |
化为ab＜1，a2+b2＞2，
∴ab＜1＜
| a2+b2 |
| 2 |
故选：D．
点评：本题考查了基本不等式的性质，使用时注意“一正二定三相等”的法则，属于基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
函数f（x）=Asin（ωx+ϕ）+k在一个周期内的图象如图，函数f（x）解析式为（ ）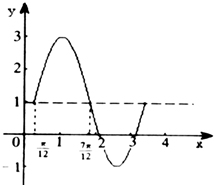
A、f（x）=4sin（
| ||||
B、f（x）=2sin（2x-
| ||||
C、f（x）=4sin（
| ||||
D、f（x）=2sin（2x-
|
己知关于x的方程（m+3）x2-4mx+2m-1=0 的两根异号，且负根的绝对值比正根大，那么实数m的取值范围是（ ）
| A、-3＜m＜0 |
| B、0＜m＜3 |
| C、m＜-3或m＞0 |
| D、m＜0 或 m＞3 |
若满足条件
的点P（x，y）构成三角形区域，则实数k取值范围是（ ）
|
| A、（-∞，-1） |
| B、（1，+∞） |
| C、（0，1） |
| D、（-∞，-1）∪（1，+∞） |
在等差数列{an}中，n≥2，公差d＜0，前n项和是Sn，则有（ ）
| A、nan＜Sn＜na1 |
| B、na1＜Sn＜nan |
| C、Sn≥na1 |
| D、Sn≤nan |
已知数列{an}中，a1=1，对所有n∈N*，都有a1a2…an=n2，则a3=（ ）
A、
| ||
| B、3 | ||
| C、9 | ||
D、
|
（1）已知矩阵M=