题目内容
在等差数列{an}中,n≥2,公差d<0,前n项和是Sn,则有( )
| A、nan<Sn<na1 |
| B、na1<Sn<nan |
| C、Sn≥na1 |
| D、Sn≤nan |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由已知的公差小于0,直接利用作差法得到答案.
解答:
解:在等差数列{an}中,
Sn=na1+
d,
∵公差d<0,∴
d<0,
则Sn<na1;
又nan-Sn=n[a1+(n-1)d]-na1-
d=
d<0.
∴nan<Sn<na1.
故选:A.
Sn=na1+
| n(n-1) |
| 2 |
∵公差d<0,∴
| n(n-1) |
| 2 |
则Sn<na1;
又nan-Sn=n[a1+(n-1)d]-na1-
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
∴nan<Sn<na1.
故选:A.
点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,训练了作差法比较两个数的大小,是中档题.

练习册系列答案
相关题目
函数f(x)=
sin2(2x-
)+
的最小正周期是 ( )
| 6 |
| π |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知a,b∈R,a≠b,且a+b=2,则( )
A、ab≤
| ||
B、1<ab<
| ||
C、ab≤1≤
| ||
D、ab<1<
|
如图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写( )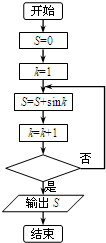

| A、k>2011? |
| B、k>2012? |
| C、k<2011? |
| D、k<2012? |
把函数y=logax的图象按向量
=(2,3)平移,得到y=f(x)的图象,则f(x)的表达式为( )
| a |
| A、f(x)=loga(x-3)+2 |
| B、f(x)=loga(x+3)-2 |
| C、f(x)=loga(x-2)+3 |
| D、f(x)=loga(x+2)-3 |
若集合M={y|x2=y,x∈R},集合N={y|x+y=0,x∈R},则M∩N等于( )
| A、{y|y∈R} |
| B、{(-1,1),(0,0)} |
| C、{(0,0)} |
| D、{x|x≥0} |