题目内容
 (1)已知矩阵M=
(1)已知矩阵M=
|
(2)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.
①求证:DE是⊙O的切线;②若
| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
(3)在极坐标系中,圆C的方程为ρ=2
| 2 |
| π |
| 4 |
|
考点:矩阵特征值的定义
专题:矩阵和变换
分析:本题(1)先根据特征多项式,利用已知的特征值,求出参数x的值,再求出另一个特征值,以及对应的一个特征向量;(2)
解答:
解:(1)∵矩阵M=
,
∴矩阵M的一个特征多项式为:f(λ)=
=(λ-1)(λ-x)-4.
∵矩阵M的一个特征值为3,
∴f(3)=0,
即(3-1)(3-x)-4=0,
∴x=1.
∴f(λ)=(λ-1)(λ-1)-4=(λ-3)(λ+1),
令f(λ)=0,
λ=3或λ=-1,
当λ=-1时,
-2x-2y=0,
取x=1,则y=-1,
∴另一个特征值为-1,对应的一个特征向量为
.
|
∴矩阵M的一个特征多项式为:f(λ)=
|
∵矩阵M的一个特征值为3,
∴f(3)=0,
即(3-1)(3-x)-4=0,
∴x=1.
∴f(λ)=(λ-1)(λ-1)-4=(λ-3)(λ+1),
令f(λ)=0,
λ=3或λ=-1,
当λ=-1时,
-2x-2y=0,
取x=1,则y=-1,
∴另一个特征值为-1,对应的一个特征向量为
|
点评:本题考查了矩阵的特征值、特征向量,本题难度不大,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知a,b∈R,a≠b,且a+b=2,则( )
A、ab≤
| ||
B、1<ab<
| ||
C、ab≤1≤
| ||
D、ab<1<
|
若集合M={y|x2=y,x∈R},集合N={y|x+y=0,x∈R},则M∩N等于( )
| A、{y|y∈R} |
| B、{(-1,1),(0,0)} |
| C、{(0,0)} |
| D、{x|x≥0} |
已知集合A={x|x<a},B={x|1≤x<2},且A∪(∁UB)=R,则实数a的取值范围是( )
| A、a≤1 | B、a<1 |
| C、a≥2 | D、a>2 |
把函数y=sin(2x+
)的图象向右平移
个单位,所得的图象对应的函数是( )
| π |
| 4 |
| π |
| 4 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
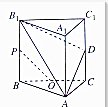 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证: