题目内容
若满足条件
的点P（x，y）构成三角形区域，则实数k取值范围是（ ）
|
| A、（-∞，-1） |
| B、（1，+∞） |
| C、（0，1） |
| D、（-∞，-1）∪（1，+∞） |
考点：简单线性规划
专题：数形结合
分析：作出不等式组对应的平面区域，根据平面区域是三角形，即可确定k的取值范围．
解答：
解：作出不等式组对应的平面区域，
直线kx-y-2k+1=0得k（x-2）+1-y=0，则直线过定点（2，1），
当直线k（x-2）+1-y=0与x+y-2=0平行时，即k=-1时，此时对应的平面区域不是三角形，
∴要使对应的平面区域是三角形，
则k（x-2）+1-y=0与x+y-2=0在第一象限内相交，即k＜-1，
故选：A．
直线kx-y-2k+1=0得k（x-2）+1-y=0，则直线过定点（2，1），当直线k（x-2）+1-y=0与x+y-2=0平行时，即k=-1时，此时对应的平面区域不是三角形，
∴要使对应的平面区域是三角形，
则k（x-2）+1-y=0与x+y-2=0在第一象限内相交，即k＜-1，
故选：A．
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
函数f(x)=
sin2(2x-
)+
的最小正周期是 （ ）
| 6 |
| π |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知a，b∈R，a≠b，且a+b=2，则（ ）
A、ab≤
| ||
B、1＜ab＜
| ||
C、ab≤1≤
| ||
D、ab＜1＜
|
如图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图，则在判断框中填写（ ）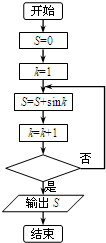
| A、k＞2011？ |
| B、k＞2012？ |
| C、k＜2011？ |
| D、k＜2012？ |