Question

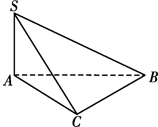如图，已知SA⊥Rt△ABC，BC⊥AC，∠ABC=30°，AC=1，SB=2

3

，求SC与平面SAB所成角的正弦值．

Answer 1

考点：直线与平面所成的角

专题：计算题,作图题,空间位置关系与距离

分析：在Rt△ABC中作CD⊥AB于点D，连结SD，可证明∠CSD为SC与平面SAB所成的角，在Rt△ABC，Rt△SBC，Rt△SDC中求边长，从而求SC与平面SAB所成角的正弦值．

解答： 解：在Rt△ABC中作CD⊥AB于点D，连结SD，
∵SA⊥Rt△ABC，
又∵SA?面SAB，
∴面SAB⊥面ABC，
又∵面SAB∩面ABC=AB，
∴CD⊥面SAB，
∴∠CSD为SC与平面SAB所成的角，
在Rt△ABC中，
∵BC⊥AC，∠ABC=30°，AC=1，
∴BC=

3

，AB=2；
∴CD=

3 ×1

2

=

3

2

，
在Rt△SBC中，
SB=2

3

，BC=

3

，
则SC=

12-3

=3，
在Rt△SDC中，
sin∠CSD=

CD

SC

=

3 2

3

=

3

6

．

点评：本题考查了学生的空间想象力及作图能力、计算能力，属于中档题．