题目内容
在双曲线
-
=1的两条渐近线上分别取点A、B,使得|
|•|
|=c2,则线段AB中点P的轨迹方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可得双曲线
-
=1的渐近线方程为y=±
x,从而设A(m,
m),B(n,-
n);从而可得
•
=c2,化简可得|mn|=a2,令
=x,
(
)=y,从而解得m=x+
y,n=(x-
y),从而解得
-
=1或
-
=-1.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
| b |
| a |
m2+
|
n2+
|
| m+n |
| 2 |
| b |
| a |
| m-n |
| 2 |
| a |
| b |
| a |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:∵双曲线
-
=1的渐近线方程为y=±
x,
∴设A(m,
m),B(n,-
n);
∴P(
,
(
));
则由|
|•|
|=c2可得,
•
=c2,
即
|mn|=c2,
则|mn|=a2,
令
=x,
(
)=y,
则m=x+
y,n=(x-
y),
则上式可化为
|(x+
y)(x-
y)|=a2,
故
-
=1或
-
=-1.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
∴设A(m,
| b |
| a |
| b |
| a |
∴P(
| m+n |
| 2 |
| b |
| a |
| m-n |
| 2 |
则由|
| OA |
| OB |
m2+
|
n2+
|
即
| c2 |
| a2 |
则|mn|=a2,
令
| m+n |
| 2 |
| b |
| a |
| m-n |
| 2 |
则m=x+
| a |
| b |
| a |
| b |
则上式可化为
|(x+
| a |
| b |
| a |
| b |
故
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
点评:本题考查了双曲线的应用,同时考查了轨迹方程的求法,属于难题.

练习册系列答案
相关题目
已知球的体积是
π,那么球的半径等于( )
| 32 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
已知等差数列{an}中,a2=3,a4=7,则数列{an}的前5项之和等于( )
| A、30 | B、25 | C、20 | D、16 |
抛物线y=ax2的准线方程为x=1,则实数a的值为( )
| A、4 | ||
B、
| ||
C、-
| ||
| D、-4 |
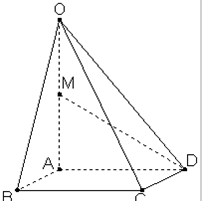 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.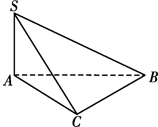 如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2
如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2