题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,若A=
,且
•
=4,则△ABC的面积等于 .
| π |
| 3 |
| AC |
| AB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由已知A=
,且
•
=4,根据向量数量积的公式算出AB×AC=8.再利用正弦定理的面积公式,即可算出△ABC的面积.
| π |
| 3 |
| AC |
| AB |
解答:
解:∵A=
,且
•
=4,∴AB×AC×ccosA=4,得AB×AC=8
因此,△ABC的面积S=
AB×ACsinA=
×8×
=2
;
故答案为:2
.
| π |
| 3 |
| AC |
| AB |
因此,△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了平面向量得数量积得运用以及求三角形的面积等知识,属于基础题.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,平面A1BD与平面C1BD所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=3,则直线A1C与平面ABC1D1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y=ax2的准线方程为x=1,则实数a的值为( )
| A、4 | ||
B、
| ||
C、-
| ||
| D、-4 |
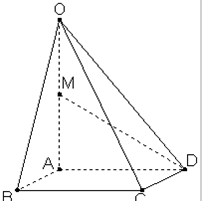 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.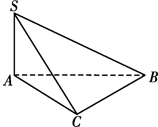 如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2
如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2