题目内容
正方体ABCD-A1B1C1D1中,求证:
(1)B1C1∥平面A1BC;
(2)AB1⊥平面A1BC.
(1)B1C1∥平面A1BC;
(2)AB1⊥平面A1BC.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由B1C1∥BC,BC?平面A1BC,B1C1?平面A1BC,从而由直线与平面平行的判定定理可知:B1C1∥平面A1BC;
(2)由BC⊥平面A1B1BA,AB1?平面A1B1BA,有BC⊥AB1又由AB1⊥A1B,A1B∩BC=B,从而可证AB1⊥平面A1BC.
(2)由BC⊥平面A1B1BA,AB1?平面A1B1BA,有BC⊥AB1又由AB1⊥A1B,A1B∩BC=B,从而可证AB1⊥平面A1BC.
解答:

证明:(1)∵正方体ABCD-A1B1C1D1中,B1C1∥BC,BC?平面A1BC,B1C1?平面A1BC,
∴由直线与平面平行的判定定理可知:B1C1∥平面A1BC;
(2)∵BC⊥平面A1B1BA,AB1?平面A1B1BA,
∴BC⊥AB1
又∵AB1⊥A1B,A1B∩BC=B
∴AB1⊥平面A1BC.

证明:(1)∵正方体ABCD-A1B1C1D1中,B1C1∥BC,BC?平面A1BC,B1C1?平面A1BC,
∴由直线与平面平行的判定定理可知:B1C1∥平面A1BC;
(2)∵BC⊥平面A1B1BA,AB1?平面A1B1BA,
∴BC⊥AB1
又∵AB1⊥A1B,A1B∩BC=B
∴AB1⊥平面A1BC.
点评:本题主要考察了直线与平面平行的判定,直线与平面垂直的判定,属于基本知识的考查.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,平面A1BD与平面C1BD所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知球的体积是
π,那么球的半径等于( )
| 32 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
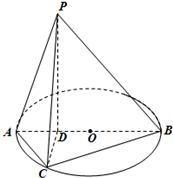 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.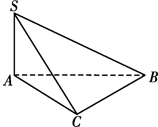 如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2
如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2