题目内容
设函数f(x)=sinx+cosx•sinφ(|φ|<
)在x=
处取得极值,则cosφ的值为 .
| π |
| 2 |
| π |
| 3 |
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用,三角函数的求值
分析:求出函数的导数,由于f(x)在x=
处取得极值,则有f′(
)=0,再由同角的平方关系,即可得到所求值.
| π |
| 3 |
| π |
| 3 |
解答:
解:函数f(x)=sinx+cosx•sinφ的导数为
f′(x)=cosx-sinx•sinφ
由于f(x)在x=
处取得极值,则有f′(
)=0,
即有cos
-sin
•sinφ=0,即sinφ=
,
由于|φ|<
,则cosφ=
=
.
故答案为:
.
f′(x)=cosx-sinx•sinφ
由于f(x)在x=
| π |
| 3 |
| π |
| 3 |
即有cos
| π |
| 3 |
| π |
| 3 |
| ||
| 3 |
由于|φ|<
| π |
| 2 |
1-(
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查函数的导数的运用:求极值,考查三角函数的化简和求值,考查运算能力,属于基础题.

练习册系列答案
相关题目
集合A={x|x=-y2+6,x∈N,y∈N}的真子集的个数为( )
| A、9 | B、8 | C、7 | D、6 |
在正方体ABCD-A1B1C1D1中,平面A1BD与平面C1BD所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知球的体积是
π,那么球的半径等于( )
| 32 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
已知等差数列{an}中,a2=3,a4=7,则数列{an}的前5项之和等于( )
| A、30 | B、25 | C、20 | D、16 |
已知正实数a,b满足
+
=1,x=a+b,则实数x的取值范围是( )
| 2 |
| a |
| 1 |
| b |
| A、[6,+∞) | ||
B、{2
| ||
C、[4
| ||
D、[3+2
|
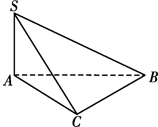 如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2
如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2