题目内容
 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=
| ||
| 3 |
(1)求PA的长;
(2)求证:MN∥平面PAB;
(3)试在AB上找一点F,使EF∥平面PAD;
(4)求线段MN的长的最小值.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)设出PA,利用勾股定理以及三角形的面积求解即可.
(2)过M作MR∥PA,连结NR,说明平面MNR∥平面PAB,即可得到结论.
(3)画出图形,过E作EG∥CD交PD于G,连接AG,在AB上取点F,使AF=EG,要证明EF∥平面PAD,只需证明FE∥AG即可;然后确定F的位置.
(4)设出PM,然后求出MR,NR,表示出MN,然后利用二次函数的最值求解最小值.
(2)过M作MR∥PA,连结NR,说明平面MNR∥平面PAB,即可得到结论.
(3)画出图形,过E作EG∥CD交PD于G,连接AG,在AB上取点F,使AF=EG,要证明EF∥平面PAD,只需证明FE∥AG即可;然后确定F的位置.
(4)设出PM,然后求出MR,NR,表示出MN,然后利用二次函数的最值求解最小值.
解答:
 解:(1)由题意设PA=x,则:PB=
解:(1)由题意设PA=x,则:PB=
,AC=
a,PC=
,在Rt△PBC中,BE•PB=BC•PB
可得:
a•
=a•
,解得x=a.
∴PA=a.
(2)过M作MR∥PA,连结NR,由(1)可知PA=a,
M、N分别为PD、AC上的点,且PM=AN.
易证NR∥CD,可得平面MNR∥平面PAB,
⇒MN∥平面PAB;
(3) 解:在平面PCD内,过E作EG∥CD交PD于G,连接AG,
解:在平面PCD内,过E作EG∥CD交PD于G,连接AG,
在AB上取点F,使AF=EG,则F即为所求作的点.
∵EG∥CD∥AF,EG=AF,
∴四边形FEGA为平行四边形,
∴FE∥AG.
又AG?平面PAD,FE?平面PAD,
∴EF∥平面PAD.
又在Rt△BCE中,
CE=
=
a.
在Rt△PBC中,BC2=CE•CP
∴CP=
=
a.又
=
,
∴EG=
•CD=
a,
∴AF=EG=
a.
∴点F为AB的一个三等分点.
(4)设PM=t,(0<t<
a),则AN=t,∵NR∥CD,可知
△ANR∽△ACD,∴
=
,NR=
t.
同理可得MR=a-
t.
MN=
=
,(0<t<
a),
当t=
a时,MN最小,最小值为:
a.
 解:(1)由题意设PA=x,则:PB=
解:(1)由题意设PA=x,则:PB=| x2+a2 |
| 2 |
| x2+2a2 |
可得:
| ||
| 3 |
| x2+2a2 |
| x2+a2 |
∴PA=a.
(2)过M作MR∥PA,连结NR,由(1)可知PA=a,
M、N分别为PD、AC上的点,且PM=AN.
易证NR∥CD,可得平面MNR∥平面PAB,
⇒MN∥平面PAB;
(3)
 解:在平面PCD内,过E作EG∥CD交PD于G,连接AG,
解:在平面PCD内,过E作EG∥CD交PD于G,连接AG,在AB上取点F,使AF=EG,则F即为所求作的点.
∵EG∥CD∥AF,EG=AF,
∴四边形FEGA为平行四边形,
∴FE∥AG.
又AG?平面PAD,FE?平面PAD,
∴EF∥平面PAD.
又在Rt△BCE中,
CE=
| BC2-BE2 |
| ||
| 3 |
在Rt△PBC中,BC2=CE•CP
∴CP=
| a2 | ||||
|
| 3 |
| EG |
| CD |
| PE |
| PC |
∴EG=
| PE |
| PC |
| 2 |
| 3 |
∴AF=EG=
| 2 |
| 3 |
∴点F为AB的一个三等分点.
(4)设PM=t,(0<t<
| 2 |
△ANR∽△ACD,∴
| NR |
| a |
| t | ||
|
| ||
| 2 |
同理可得MR=a-
| ||
| 2 |
MN=
(
|
t2-
|
| 2 |
当t=
| ||
| 2 |
| ||
| 2 |
点评:本题考查直线与平面平行的判定,涉及空间距离,以及空间距离的最值问题,考查学生的逻辑思维能力,空间想象能力以及转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
集合A={x|x=-y2+6,x∈N,y∈N}的真子集的个数为( )
| A、9 | B、8 | C、7 | D、6 |
在正方体ABCD-A1B1C1D1中,平面A1BD与平面C1BD所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}中,a2=3,a4=7,则数列{an}的前5项之和等于( )
| A、30 | B、25 | C、20 | D、16 |
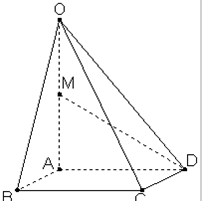 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.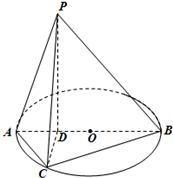 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.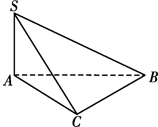 如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2
如图,已知SA⊥Rt△ABC,BC⊥AC,∠ABC=30°,AC=1,SB=2