题目内容
已知全集I=Z,集合A={x|x=2k+1,k∈Z},B={x|x=4k+1,k∈Z},则有( )
| A、I=(CIA)∪B |
| B、I=(CIB)∪B |
| C、I=(CIA)∪(CIB) |
| D、I=A∪B |
考点:交、并、补集的混合运算
专题:计算题
分析:I=(CIB)∪B,(CIB)∩B=∅,这是补集的基本性质.
解答:
解:∵全集I=Z,
集合A={x|x=2k+1,k∈Z}是全体奇数,
B={x|x=4k+1,k∈Z}是除以4余1的奇数,
∴I=(CIB)∪B.
故选B.
集合A={x|x=2k+1,k∈Z}是全体奇数,
B={x|x=4k+1,k∈Z}是除以4余1的奇数,
∴I=(CIB)∪B.
故选B.
点评:本题考查补集的基本性质的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
如果a
=b(a>0,且a≠1),则( )
| 1 |
| 2 |
A、log
| ||||
B、log
| ||||
C、log
| ||||
D、log
|
已知
ax不存在(a>0),则
的值为( )
| lim |
| x→∞ |
| lim |
| x→∞ |
| 1-ax |
| 1+ax |
| A、-1 | B、0 | C、1 | D、不存在 |
若实数x,y满足不等式
,则z=2x+y的最大值为( )
|
| A、1 | B、3 | C、4 | D、5 |
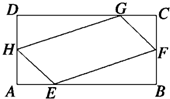 如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).
如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).