题目内容
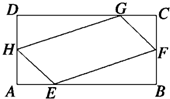 如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).
如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).(1)求f(x)的解析式和定义域;
(2)当x为何值时,四边形EFGH的面积最大?并求出最大面积.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)求出矩形四个角落的三角形的面积,再利用矩形的面积减去四个角落的三角形的面积,可得四边形EFGH的面积,即可得到f(x)的解析式和定义域;
(2)配方确定函数的对称轴,与函数的定义域结合,分类求出四边形EFGH的面积最大值.
(2)配方确定函数的对称轴,与函数的定义域结合,分类求出四边形EFGH的面积最大值.
解答:
解:(1)由题意,S△AHE=S△CGF=
x2,S△DGH=S△BEF=
(a-x)(b-x)
∴f(x)=SEFGH=ab-2[
x2+
(a-x)(b-x)]=-2x2+(a+b)x(0<x≤b)
(2)f(x)=-2x2+(a+b)x=-2(x-
)2+
(0<x≤b)
若
≤b,即b<a≤3b时,当x=
时,f(x)max=
若
>b,即a>3b时,S(x)在(0,b]上为增函数,当x=b时,f(x)max=ab-b2.
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=SEFGH=ab-2[
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(x)=-2x2+(a+b)x=-2(x-
| a+b |
| 4 |
| (a+b)2 |
| 8 |
若
| a+b |
| 4 |
| a+b |
| 4 |
| (a+b)2 |
| 8 |
若
| a+b |
| 4 |
点评:本题考查四边形面积的计算,考查利用配方法求二次函数的最值,应注意函数的对称轴与区间结合,确定分类的标准.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
若关于x的方程x2+2kx+3k=0的两相异实根都在(-1,3)内,则k的取值范围是( )
| A、k≥3或k≤0 |
| B、k<-1 |
| C、k>0 |
| D、(-1,0) |
已知全集I=Z,集合A={x|x=2k+1,k∈Z},B={x|x=4k+1,k∈Z},则有( )
| A、I=(CIA)∪B |
| B、I=(CIB)∪B |
| C、I=(CIA)∪(CIB) |
| D、I=A∪B |
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题: