题目内容
不等式组
表示平面区域的面积为 .
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据二元一次不等式组作出平面区域,然后根据区域的形状求出其面积即可.
解答:
 解:∵
解:∵
∴
或
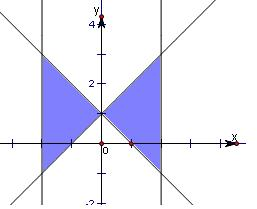
然后根据二元一次不等式组画出区域图,如右图
根据图象可知不等式组
表示的平面区域为两个全等的三角形,
可以拼成边长为4的正方形的一半,
所以面积为S=
×42=8
故答案为:8.
 解:∵
解:∵
|
∴
|
|
然后根据二元一次不等式组画出区域图,如右图
根据图象可知不等式组
|
表示的平面区域为两个全等的三角形,
可以拼成边长为4的正方形的一半,
所以面积为S=
| 1 |
| 2 |
故答案为:8.
点评:本题主要考查了二元一次不等式(组)与平面区域,以及图象面积的度量,解题的关键是作图,属于基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
已知直线mx+3y-4=0与圆(x+2)2+y2=5相交于A、B两点,若|AB|=2,则实数m的值为( )
A、
| ||||
B、0或-
| ||||
C、±
| ||||
D、
|
点A(1,2,3)在坐标平面yOz内的射影是点B的坐标是( )
| A、(0,2,3) |
| B、(1,0,3) |
| C、(1,2,0) |
| D、(1,0,0) |
已知全集I=Z,集合A={x|x=2k+1,k∈Z},B={x|x=4k+1,k∈Z},则有( )
| A、I=(CIA)∪B |
| B、I=(CIB)∪B |
| C、I=(CIA)∪(CIB) |
| D、I=A∪B |
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题: