题目内容
将参加夏令营的600名学生编号为：001，002，…，600．采用系统抽样方法抽取一个容量为50的样本，且已知随机抽得的第一个号码为003．这600名学生分住在三个营区，从001到312在第一区，从313到504在第二区，从505到600在第三区．三个营区被抽中的人数依次为（ ）
| A、26，16，8 |
| B、26，17，7 |
| C、25，17，8 |
| D、25，16，9 |
考点：系统抽样方法
专题：计算题,概率与统计
分析：依题意可知，在随机抽样中，首次抽到003号，以后每隔12个号抽到一个人，则构成以3为首项，12为公差的等差数列，从而得出三个营区被抽中的人数．
解答：
解：依题意可知，在随机抽样中，首次抽到003号，以后每隔12个号抽到一个人，
则分别是003、015、027、039构成以3为首项，12为公差的等差数列，
故可分别求出在001到312中有26人，在313至504号中共有16人，则505到600中有8人．
故选：A．
则分别是003、015、027、039构成以3为首项，12为公差的等差数列，
故可分别求出在001到312中有26人，在313至504号中共有16人，则505到600中有8人．
故选：A．
点评：本题考查系统抽样方法，本题解题的关键是看出每一个组里的人数，属于基础题．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
已知a，b为正实数，函数f（x）=ax3+bx+2在[0，1]上的最大值为4，则f（x）在[-1，0]上的最小值为（ ）
| A、0 | ||
B、
| ||
| C、-2 | ||
| D、2 |
设x∈R，2 x2-1＞4则不等式的解是（ ）
A、x≠±
| ||||
B、-
| ||||
| C、-2＜x＜2 | ||||
D、x＞
|
已知函数f（x）=loga（2x+b-1）（a＞0且a≠1）的图象如图所示，则a、b满足的关系式是（ ）
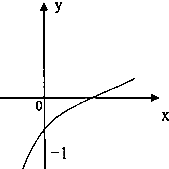
A、0＜b＜
| ||||
B、0＜
| ||||
C、0＜
| ||||
D、0＜
|
已知点A、B、C三点不共线，且有
=
=
，则有（ ）
| ||||
| 1 |
| ||||
|
| ||||
|
A、|
| ||||||
B、|
| ||||||
C、|
| ||||||
D、|
|
直线l过点P（-2，0）且与圆x2+y2=1相切，则l的斜率是（ ）
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|
已知函数f（x）=x3+bx2+cx+d（b、c、d为常数），当x∈（0，1）时取得极大值，当x∈（1，2）时取极小值，则（b+
）2+（c-3）2的取值范围是（ ）
| 1 |
| 2 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
| D、（5，25） |
设函数f（x）=
，其中[x]表示不超过x的最大整数，如[-1.6]=-2，[1]=1，[1.2]=1，若直线y=kx+1（k＜0）与函数y=f（x）的图象恰有2个不同的交点，则k的取值范围是（ ）
|
A、[-
| ||||
B、[-1，-
| ||||
C、（-1，-
| ||||
D、（-
|