题目内容
已知函数f(x)=x3+bx2+cx+d(b、c、d为常数),当x∈(0,1)时取得极大值,当x∈(1,2)时取极小值,则(b+
)2+(c-3)2的取值范围是( )
| 1 |
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(5,25) |
考点:利用导数研究函数的极值
专题:综合题,导数的概念及应用
分析:据极大值点左边导数为正右边导数为负,极小值点左边导数为负右边导数为正得a,b的约束条件,据线性规划求出最值.
解答:
 解:∵f(x)=x3+bx2+cx+d,
解:∵f(x)=x3+bx2+cx+d,
∴f′(x)=3x2+2bx+c,
∵函数f(x)在x∈(0,1)时取得极大值,当x∈(1,2)时取极小值,
∴f′(x)=3x2+2bx+c=0在(0,1)和(1,2)内各有一个根,
∴f′(0)>0,f′(1)<0,f′(2)>0,
即
,
在bOc坐标系中画出其表示的区域,如图,
(b+
)2+(c-3)2表示点A(-
,3)与可行域内的点连线的距离的平方,
点A(-
,3)到直线3+2b+c=0的距离为
=
,
由12+4b+c=0与3+2b+c=0联立,可得交点为(-4.5,6),与点A(-
,3)的距离为5,
∴(b+
)2+(c-3)2的取值范围是(5,25),
故选:D.
 解:∵f(x)=x3+bx2+cx+d,
解:∵f(x)=x3+bx2+cx+d,∴f′(x)=3x2+2bx+c,
∵函数f(x)在x∈(0,1)时取得极大值,当x∈(1,2)时取极小值,
∴f′(x)=3x2+2bx+c=0在(0,1)和(1,2)内各有一个根,
∴f′(0)>0,f′(1)<0,f′(2)>0,
即
|
在bOc坐标系中画出其表示的区域,如图,
(b+
| 1 |
| 2 |
| 1 |
| 2 |
点A(-
| 1 |
| 2 |
| |-1+3+3| | ||
|
| 5 |
由12+4b+c=0与3+2b+c=0联立,可得交点为(-4.5,6),与点A(-
| 1 |
| 2 |
∴(b+
| 1 |
| 2 |
故选:D.
点评:考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
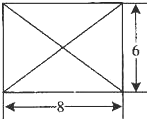 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )| A、48 | B、64 | C、96 | D、192 |
将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且已知随机抽得的第一个号码为003.这600名学生分住在三个营区,从001到312在第一区,从313到504在第二区,从505到600在第三区.三个营区被抽中的人数依次为( )
| A、26,16,8 |
| B、26,17,7 |
| C、25,17,8 |
| D、25,16,9 |
下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )
| A、y=x-2 | ||
| B、y=x-1 | ||
C、y=(
| ||
D、y=log
|
三个数a=70.3,b=0.37,c=ln0.3的大小关系是( )
| A、a>c>b |
| B、a>b>c |
| C、b>a>c |
| D、c>a>b |
等差数列{an}中,若S4≤4,S5≥15,则a4的最小值是( )
| A、5 | B、6 | C、7 | D、8 |
若α=kπ+
(k∈z),则α在( )
| π |
| 4 |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、四象限 |
| D、第三、四象限 |
i是虚数单位,
=( )
| 3-4i |
| 1+2i |
A、
| ||
B、
| ||
| C、-1+2i | ||
| D、-1-2i |
函数f(x)=x5-x-1在下列区间一定有零点的是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |