题目内容
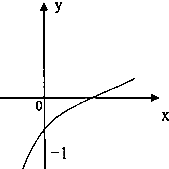
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的图象如图所示,则a、b满足的关系式是( )

A、0<b<
| ||||
B、0<
| ||||
C、0<
| ||||
D、0<
|
考点:函数的图象
专题:函数的性质及应用
分析:利用对数函数和函数图象平移的方法列出关于a,b的不等关系是解决本题的关键.利用好图形中的标注的(0,-1)点.利用复合函数思想进行单调性的判断,进而判断出底数与1的大小关系.
解答:
解:∵函数f(x)=loga(2x+b-1)是增函数且随着x增大,2x+b-1增大,f(x)也增大.
∴a>1,∴0<
<1,
∵当x=0时,f(0)=logab<0,
∴0<b<1.
又∵f(0)=logab>-1=loga
,
∴b>
,
∴0<
<b<1.
故选:B.
∴a>1,∴0<
| 1 |
| a |
∵当x=0时,f(0)=logab<0,
∴0<b<1.
又∵f(0)=logab>-1=loga
| 1 |
| a |
∴b>
| 1 |
| a |
∴0<
| 1 |
| a |
故选:B.
点评:本题考查对数函数的图象性质,考查学生的识图能力.考查学生的数形结合能力和等价转化思想.

练习册系列答案
相关题目
方程2012x+2013x+2014x=2015x
的实根个数为( )
| x-2016 |
| A、0个 | B、1个 |
| C、2个 | D、至少3个 |
一个中袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八张卡片,现从中无放回地每次抽一张卡片,共抽2次,则取得两张卡片的编号和不小于14的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=x2-2x的定义域为{0,1,2,3},那么f(x)的值域为( )
| A、{-1,0,3} |
| B、{0,1,2,3} |
| C、{y|-1≤y≤3} |
| D、{y|0≤y≤3} |
将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且已知随机抽得的第一个号码为003.这600名学生分住在三个营区,从001到312在第一区,从313到504在第二区,从505到600在第三区.三个营区被抽中的人数依次为( )
| A、26,16,8 |
| B、26,17,7 |
| C、25,17,8 |
| D、25,16,9 |
从2009名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2009人中剔除9人,剩下的2000人再按系统抽样的方法抽取50人,则在2009人中,每人入选的概率( )
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等,且为
| ||
D、都相等,且为
|
三个数a=70.3,b=0.37,c=ln0.3的大小关系是( )
| A、a>c>b |
| B、a>b>c |
| C、b>a>c |
| D、c>a>b |
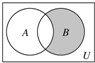 已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )
已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )| A、{0} | B、{2} |
| C、{4} | D、{2,4} |