题目内容
已知数列{an}中,a1=
,an+1=1-
(n≥2),则a2014= .
| 1 |
| 2 |
| 1 |
| an |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由首项和数列递推式分别求得a2,a3,a4,得到数列{an}是一个每三次循环的数列,周期为3,然后由数列的周期性得答案.
解答:
解:由a1=
,an+1=1-
(n≥2),得
a2=1-
=1-
=-1.
a3=1-
=1-
=2.
a4=1-
=1-
=
=a1.
由上式可知,{an}是一个每三次循环的数列,周期为3,
∴有a2014=a671×3+1=a1=
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| an |
a2=1-
| 1 |
| a1 |
| 1 | ||
|
a3=1-
| 1 |
| a2 |
| 1 |
| -1 |
a4=1-
| 1 |
| a3 |
| 1 |
| 2 |
| 1 |
| 2 |
由上式可知,{an}是一个每三次循环的数列,周期为3,
∴有a2014=a671×3+1=a1=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了数列递推式,关键是发现数列的周期性,是中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
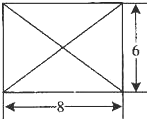 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为( )| A、48 | B、64 | C、96 | D、192 |
将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且已知随机抽得的第一个号码为003.这600名学生分住在三个营区,从001到312在第一区,从313到504在第二区,从505到600在第三区.三个营区被抽中的人数依次为( )
| A、26,16,8 |
| B、26,17,7 |
| C、25,17,8 |
| D、25,16,9 |
