题目内容
设函数f(x)=
,其中[x]表示不超过x的最大整数,如[-1.6]=-2,[1]=1,[1.2]=1,若直线y=kx+1(k<0)与函数y=f(x)的图象恰有2个不同的交点,则k的取值范围是( )
|
A、[-
| ||||
B、[-1,-
| ||||
C、(-1,-
| ||||
D、(-
|
考点:分段函数的应用,函数的图象
专题:函数的性质及应用
分析:若f(x)=kx+1与f(x)有2个不同的交点,画出函数f(x)的图象,结合y=kx+1的图象恒过(0,1)点,数形结合,易分析出k的取值范围.
解答:
解:当-1≤x<0,[x]=-1,此时f(x)=x+1,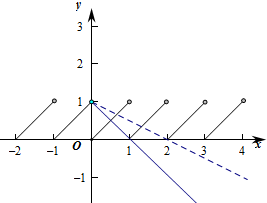
当0≤x<1,-1≤x-1<0,f(x)=f(x-1)=x,
当x>0时,函数的周期为1,作出函数f(x)的图象如图:
∵直线y=kx+1(k<0)过定点(0,1),
∴由图象可知当直线经过点(1,0)时,两个函数的图象有2个交点,此时0=k+1,
解得k=-1,
当直线经过点(2,0)时,两个图象有3个交点,此时0=2k+1,解得k=-
,但此时不满足条件,
故要使直线y=kx+1(k<0)与函数y=f(x)的图象恰有2个不同的交点,
则-1≤x<-
,
故选:B

当0≤x<1,-1≤x-1<0,f(x)=f(x-1)=x,
当x>0时,函数的周期为1,作出函数f(x)的图象如图:
∵直线y=kx+1(k<0)过定点(0,1),
∴由图象可知当直线经过点(1,0)时,两个函数的图象有2个交点,此时0=k+1,
解得k=-1,
当直线经过点(2,0)时,两个图象有3个交点,此时0=2k+1,解得k=-
| 1 |
| 2 |
故要使直线y=kx+1(k<0)与函数y=f(x)的图象恰有2个不同的交点,
则-1≤x<-
| 1 |
| 2 |
故选:B
点评:本题考查的知识点是根据根的存在性及根的个数的判断,利用图象法结合数形结合的思想,分析函数图象交点与k的关系是解答本题的关键.

练习册系列答案
相关题目
将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且已知随机抽得的第一个号码为003.这600名学生分住在三个营区,从001到312在第一区,从313到504在第二区,从505到600在第三区.三个营区被抽中的人数依次为( )
| A、26,16,8 |
| B、26,17,7 |
| C、25,17,8 |
| D、25,16,9 |
若α=kπ+
(k∈z),则α在( )
| π |
| 4 |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、四象限 |
| D、第三、四象限 |
i是虚数单位,
=( )
| 3-4i |
| 1+2i |
A、
| ||
B、
| ||
| C、-1+2i | ||
| D、-1-2i |
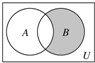 已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )
已知全集U=N,A={0,1,2},B={y|y=2x,x∈A},则图中的阴影部分所表示的集合等于( )| A、{0} | B、{2} |
| C、{4} | D、{2,4} |
将函数f(x)=sin(2x+
)的图象向右平移
个单位后得到函y=g(x)的图象,则g(x)的单调递增区间为( )
| π |
| 3 |
| π |
| 4 |
A、[2kπ-
| ||||
B、[2kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
函数f(x)=x-4+log2x的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
函数f(x)=x5-x-1在下列区间一定有零点的是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |