题目内容
已知an=
,求前n项和.
| n(n+1) |
| 6 |
考点:数列的求和
专题:等差数列与等比数列
分析:an=
=
n2+
n.而12+22+32+…+n2=
,1+2+3+…+n=
.代入即可得出.
| n(n+1) |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
解答:
解:an=
=
n2+
n.
∵12+22+32+…+n2=
,
1+2+3+…+n=
.
∴Sn=
×
+
×
=
=
.
| n(n+1) |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
∵12+22+32+…+n2=
| n(n+1)(2n+1) |
| 6 |
1+2+3+…+n=
| n(n+1) |
| 2 |
∴Sn=
| 1 |
| 6 |
| n(n+1)(2n+1) |
| 6 |
| 1 |
| 6 |
| n(n+1) |
| 2 |
=
| n(n+1)(2n+1)+3(n+1)n |
| 36 |
=
| n(n+1)(n+2) |
| 18 |
点评:本题考查了等差数列的前n项和公式、与12+22+32+…+n2=
,考查了推理能力与计算能力,属于中档题.
| n(n+1)(2n+1) |
| 6 |

练习册系列答案
相关题目
某市缺水问题比较突出,为了制定水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x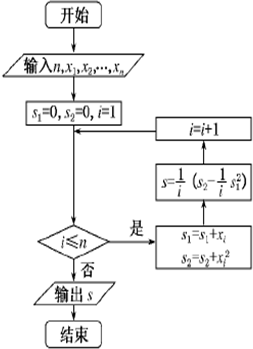 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知x,y为正实数,则下列各关系式正确的是( )
| A、2lgx+lgy=2lgx+2lgy |
| B、2lg(x+y)=2lgx•2lgy |
| C、2lgx•lgy=2lgx+2lgy |
| D、2lg(xy)=2lgx•2lgy |