题目内容
若非零向量
，
满足|
+
|=|
-
|=2|
|，则
+
与
-
的夹角是 ．
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的平方即为模的平方，可得
•
=0，
2=3
2，再由向量的夹角公式计算即可得到．
| a |
| b |
| a |
| b |
解答：
解：非零向量
，
满足|
+
|=|
-
|=2|
|，
则（
+
）2=（
-
）2=4
2，
即为
2+
2+2
•
=
2+
2-2
•
=4
2，
则
•
=0，
2=3
2，
cos＜
+
，
-
＞=
=
=
．
由0≤＜
+
，
-
＞≤π，
则＜
+
，
-
＞=
．
故答案为：
．
| a |
| b |
| a |
| b |
| a |
| b |
| b |
则（
| a |
| b |
| a |
| b |
| b |
即为
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
则
| a |
| b |
| a |
| b |
cos＜
| a |
| b |
| a |
| b |
(
| ||||||||
|
|
| ||||
4
|
| 1 |
| 2 |
由0≤＜
| a |
| b |
| a |
| b |
则＜
| a |
| b |
| a |
| b |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查平面向量的数量积的定义和性质，考查向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
相关题目
下列函数为奇函数的是（ ）
A、y=x
| ||
| B、y=lgx2 | ||
| C、1og2x | ||
D、y=2x-
|
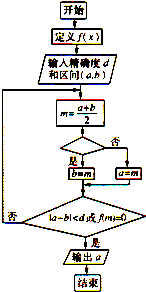已知图象不间断函数f（x）是区间[a，b]上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，判断框内可以填写的内容有如下四个选择：