题目内容
（1）求关于x的不等式x2-3ax+2a2＜0的解集．
（2）若p：实数x满足1＜x＜4是q：实数x满足x2-3ax+2a2＜0的必要条件，求实数a的取值范围．
（2）若p：实数x满足1＜x＜4是q：实数x满足x2-3ax+2a2＜0的必要条件，求实数a的取值范围．
考点：必要条件、充分条件与充要条件的判断,一元二次不等式的解法
专题：不等式的解法及应用,简易逻辑
分析：（1）求关于x的不等式x2-3ax+2a2＜0的解集．
（2）根据充分条件和必要条件的定义建立条件关系即可．
（2）根据充分条件和必要条件的定义建立条件关系即可．
解答：
解：（1）x2-3ax+2a2＜0等价为（x-a）（x-2a）＜0，
若a=0，则不等式的解集为∅，
若a＞0，则不等式的解集为（a，2a），
若a＜0，则不等式的解集为（2a，a）．
（2）若p是q的必要条件，
则q⇒p，
若a=0时，满足条件，
若a＞0时，满足
，解得
，
故1≤a≤2，综上a=0或1≤a≤2．
若a=0，则不等式的解集为∅，
若a＞0，则不等式的解集为（a，2a），
若a＜0，则不等式的解集为（2a，a）．
（2）若p是q的必要条件，
则q⇒p，
若a=0时，满足条件，
若a＞0时，满足
|
|
故1≤a≤2，综上a=0或1≤a≤2．
点评：本题主要考查一元二次不等式的解法以及充分条件和必要条件的应用，注意要进行分类讨论．
练习册系列答案
快捷英语周周练系列答案
相关题目
阅读如图的程序框图，运行相应的程序，则输出S的值为（ ）
| A、8 | B、18 | C、26 | D、80 |
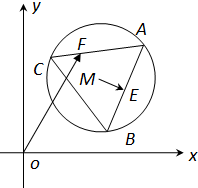如图，已知圆M：（x-3）2+（y-3）2=4，△ABC为圆M的内接正三角形，E为边AB的中点，当正△ABC绕圆心M转动，同时点F在边AC上运动时，已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
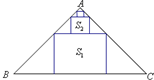在等腰直角△ABC中，∠A=90°，BC=3，△ABC中排列着内接正方形，如图所示，若正方形的面积依次为S1，S2，…，Sn，…（从大到小），其中n∈N*，则