题目内容
已知扇形的周长为4,则该扇形的面积的最大值为 .
考点:扇形面积公式
专题:三角函数的求值
分析:设扇形的半径为r,圆心角为α,则2r+rα=4,可得该扇形的面积S=
α•r2=
×(
-2)r2=-(r-1)2+1,利用二次函数的单调性即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| r |
解答:
解:设扇形的半径为r,圆心角为α,则2r+rα=4,
∴该扇形的面积S=
α•r2=
×(
-2)r2=-r2+2r=-(r-1)2+1≤1,
当且仅当r=1,α=2时取等号.
∴该扇形的面积的最大值为1.
故答案为:1.
∴该扇形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| r |
当且仅当r=1,α=2时取等号.
∴该扇形的面积的最大值为1.
故答案为:1.
点评:本题考查了弧长公式与扇形的面积计算公式、二次函数的单调性,考查了计算能力,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知变量x,y,满足约束条件
,则z=3x+y的最大值为( )
|
| A、3 | ||
| B、12 | ||
C、
| ||
| D、10 |
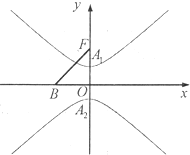 已知点A1,A2是双曲线
已知点A1,A2是双曲线| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||||
B、(1,
| ||||||
C、(
| ||||||
D、(
|
对任意实数k,直线kx-y-3k+4=0与圆C:(x-3)2+(y-4)2=16的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、与k取值有关 |
已知函数g(x)=a-x2(
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| 1 |
| e |
A、[1,
| ||
| B、[1,e2-2] | ||
C、[
| ||
| D、[e2-2,+∞) |