题目内容
对任意实数k,直线kx-y-3k+4=0与圆C:(x-3)2+(y-4)2=16的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、与k取值有关 |
考点:直线与圆的位置关系
专题:直线与圆
分析:由已知得到圆的圆心为(3,4),判断圆心到直线的距离与半径比较即可.
解答:
解:由已知圆的圆心为(3,4),它到直线kx-y-3k+4=0的距离为
=0,所以直线过圆心,由此直线与圆相交;
故选A.
| |3k-4-3k+4| | ||
|
故选A.
点评:本题考查了直线与圆的位置关系的判断;只要利用点到直线的距离公式得到圆心到直线的距离,然后与半径比较,小于半径相交;等于半径相切,大于半径相离.

练习册系列答案
相关题目
函数f(x)=asinx+blog2(x+
)+4(a、b为常数),若f(x)在(0,+∞)上有最小值-4,则f(x)在(-∞,0)上有( )
| x2+1 |
| A、最大值-2 |
| B、最大值 4 |
| C、最大值10 |
| D、最大值12 |
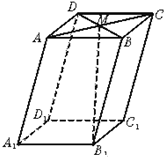 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若| A1B1 |
| a |
| A1D1 |
| b |
| A1A |
| c |
| B1M |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、-
|
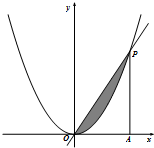 如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为
如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为