题目内容
已知4名男生、4名女生排成一排,求:
(1)男女相间有多少种排法?
(2)女生在一起有多少种排法?
(3)男生甲、乙不相邻有多少种排法?
(1)男女相间有多少种排法?
(2)女生在一起有多少种排法?
(3)男生甲、乙不相邻有多少种排法?
考点:计数原理的应用
专题:排列组合
分析:(1)先排4名男生,形成5个间隔,插入4个女生即可,
(2)先把4个女生捆绑在一起,再和4名男生全排即可,
(3)先排除甲乙之外的6人形成7个间隔,插入甲乙即可
(2)先把4个女生捆绑在一起,再和4名男生全排即可,
(3)先排除甲乙之外的6人形成7个间隔,插入甲乙即可
解答:
解:(1)先排4名男生,形成5个间隔,插入4个女生,故男女相间有
•
=2880种排法;
(2)先把4个女生捆绑在一起,再和4名男生全排,故女生在一起有
•
=2880种排法;
(3)先排除甲乙之外的6人形成7个间隔,插入甲乙,故男生甲、乙不相邻有
•
=30240种排法;
| A | 4 4 |
| A | 4 5 |
(2)先把4个女生捆绑在一起,再和4名男生全排,故女生在一起有
| A | 4 4 |
| A | 5 5 |
(3)先排除甲乙之外的6人形成7个间隔,插入甲乙,故男生甲、乙不相邻有
| A | 6 6 |
| A | 2 7 |
点评:本题考查排列问题,相邻问题用捆绑,不相邻问题用插空,属于基础题

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
函数y=x-
的大致图象为( )
| 3 | x |
A、 |
B、 |
C、 |
D、 |
函数f(x)=asinx+blog2(x+
)+4(a、b为常数),若f(x)在(0,+∞)上有最小值-4,则f(x)在(-∞,0)上有( )
| x2+1 |
| A、最大值-2 |
| B、最大值 4 |
| C、最大值10 |
| D、最大值12 |
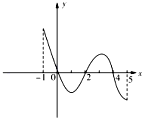 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
| A、[1,2) |
| B、[1,2] |
| C、(2,3) |
| D、[1,3) |