题目内容
16．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）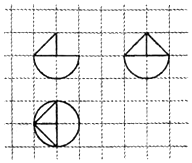
| A． | 3π+$\sqrt{3}$ | B． | 3π+$\sqrt{3}$+1 | C． | 5π+$\sqrt{3}$ | D． | 5π+$\sqrt{3}$+1 |
分析 由三视图得到几何体是半个球与三棱锥的组合体，根据图中数据计算表面积即可．
解答 
解：由题意，几何体如图：
由特征数据得到表面积为$\frac{1}{2}×4π×{1}^{2}$+π×12$+\frac{1}{2}×2×1$$+\frac{\sqrt{3}}{4}×（\sqrt{2}）^{2}×2$-$\frac{1}{2}×2×1$=3$π+\sqrt{3}$；
故选：A．
点评 本题考查了由几何体的三视图求几何体的表面积；关键是还原几何体，利用公式求表面积．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4．若a，b∈R，i是虚数单位，且b+（a-1）i=1+i，则a+b的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
11．将函数$f（x）=2sin（\frac{x}{3}-\frac{π}{6}）$的图象向左平移$\frac{π}{4}$个单位，再向上平移2个单位，得到函数g（x）的图象，则g（x）的解析式为（ ）
| A． | $g（x）=2sin（\frac{x}{3}-\frac{π}{4}）-2$ | B． | $g（x）=2sin（\frac{x}{3}+\frac{π}{4}）+2$ | C． | $g（x）=2sin（\frac{x}{3}-\frac{π}{12}）+2$ | D． | $g（x）=2sin（\frac{x}{3}-\frac{π}{12}）-2$ |
1．已知i为虚数单位，若复数$z=\frac{1-ti}{1+i}$在复平面内对应的点在第四象限，则t的取值范围为（ ）
| A． | [-1，1] | B． | （-1，1） | C． | （-∞，-1） | D． | （1，+∞） |