题目内容
8.已知实数x,y满足不等式组$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$且z=2x-y的最大值为a,则$\int_0^π{a{{cos}^2}}\frac{x}{2}dx$=3π.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用平移法进行求解得a的值,结合函数的积分公式进行求解即可.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x-y得y=2x-z,
平移直线y=2x-z,
由图象可知当直线y=2x-z经过点B时,直线y=2x-z的截距最小,
此时z最大.
由$\left\{\begin{array}{l}{y=2}\\{x-y-2=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,即B(4,2)
即a=zmax=2×4-2=6,
则$\int_0^π{a{{cos}^2}}\frac{x}{2}dx$=6∫${\;}_{0}^{π}$$\frac{1}{2}$(1+cosx)dx=3(x+sinx)|${\;}_{0}^{π}$=3π,
故答案为:3π.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想以及函数的积分公式是解决此类问题的基本方法.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )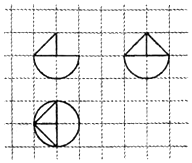

| A. | 3π+$\sqrt{3}$ | B. | 3π+$\sqrt{3}$+1 | C. | 5π+$\sqrt{3}$ | D. | 5π+$\sqrt{3}$+1 |
3.已知双曲线${C_1}:\frac{x^2}{2}-{y^2}=1$与双曲线${C_2}:\frac{x^2}{2}-{y^2}=-1$,给出下列说法,其中错误的是( )
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
20.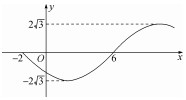 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.