题目内容
7．已知函数f（x）=x3+2x2-4x+5．求f（x）的单调区间．分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可．
解答 解：f′（x）=3x2+4x-4，
令f′（x）＞0，解得：x＞$\frac{2}{3}$或x＜-2，
令f′（x）＜0，解得：-2＜x＜$\frac{2}{3}$，
故f（x）在（-∞，-2）递增，在（-2，$\frac{2}{3}$）递减，在（$\frac{2}{3}$，+∞）递增．
点评 本题考查了函数的单调性问题，考查导数的应用，是一道基础题．
练习册系列答案
优加精卷系列答案
相关题目
在三棱柱ABC-A1B1C1中，AC=BC=2，∠ACB=120°，D为A1B1的中点．
15．若$\overrightarrow a+\overrightarrow b+\overrightarrow c=\overrightarrow 0$，且$\overrightarrow a$与$\overrightarrow c$的夹角为60°，$\overrightarrow a$与$\overrightarrow b$的夹角为θ，$|{\overrightarrow b}|=\sqrt{3}|{\overrightarrow a}|$，则tanθ=（ ）
| A． | $\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | -$\frac{{\sqrt{3}}}{3}$ | D． | -$\sqrt{3}$ |
12．2cos275°-1的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{{\sqrt{3}}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
16．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）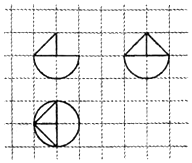
| A． | 3π+$\sqrt{3}$ | B． | 3π+$\sqrt{3}$+1 | C． | 5π+$\sqrt{3}$ | D． | 5π+$\sqrt{3}$+1 |