题目内容
6.在直角坐标系xOy中,椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$,若以直角坐标系的原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为ρ2-8ρsinθ+15=0.(1)求曲线E的普通方程和椭圆C的参数方程;
(2)已知A,B分别为两曲线上的动点,求|AB|的最大值.
分析 (1)根据x=ρcosθ,y=ρsinθ,求出曲线E的普通方程,根据cos2θ+sin2θ=1,求出椭圆C的参数方程即可;
(2)表示出AB的最大值,结合三角函数的性质求出其最大值即可.
解答 解:(1)由x=ρcosθ,y=ρsinθ得:
x2+y2-8y+15=0,即x2+(y-4)2=1,
椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$,
化为参数方程为:$\left\{\begin{array}{l}x=2cosθ\\ y=sinθ\end{array}\right.(θ$为参数).
(2)${|{AB}|_{max}}={|{AE}|_{max}}+1=\sqrt{4{{cos}^2}θ+{{({4-sinθ})}^2}}+1=\sqrt{-3{{sin}^2}θ-8sinθ+20}+1$,
由sinθ∈[-1,1],当sinθ=-1时,|AB|max=6.
点评 本题考查了参数方程和普通方程以及极坐标方程的关系,考查三角函数的性质,是一道中档题.

练习册系列答案
相关题目
16.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )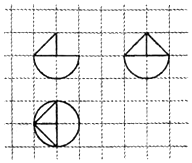

| A. | 3π+$\sqrt{3}$ | B. | 3π+$\sqrt{3}$+1 | C. | 5π+$\sqrt{3}$ | D. | 5π+$\sqrt{3}$+1 |
14.若复数z=$\frac{{{i^{2017}}}}{1-i}$(i是虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.函数f(x)=ex-4x的递减区间为( )
| A. | (0,ln4) | B. | (0,4) | C. | (-∞,ln4) | D. | (ln4,+∞) |
18.三棱锥P-ABC中,PA、PB、PC互相垂直,PA=PB=1,M是线段BC上一动点,若直线AM与平面PBC所成角的正切的最大值是$\frac{\sqrt{6}}{2}$,则三棱锥P-ABC的外接球的表面积是( )
| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
16.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)点有顶点A,O为坐标原点,以A为圆心与双曲线C的一条渐近线交于两点P,Q,若∠PAQ=60°且$\overrightarrow{OQ}$=2$\overrightarrow{OP}$,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{39}}{6}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\sqrt{3}$ |