题目内容
5.已知抛物线C:y2=4x的焦点是F,直线l1:y=x-1交抛物线于A,B两点,分别从A,B两点向直线l2:x=-2作垂线,垂足是D,C,则四边形ABCD的周长为$18+4\sqrt{2}$.分析 方法一:将直线方程代入抛物线方程,利用韦达定理及抛物线的焦点弦公式,求得丨AB丨,根据抛物线的定义,即可求得丨AD丨+丨BC丨,则丨CD丨=丨BH丨=丨AB丨×sinα,即可求得四边形ABCD的周长;
方法二:根据抛物线焦点弦的二级公式,丨AB丨=$\frac{2p}{si{n}^{2}α}$,根据抛物线的定义,即可求得丨AD丨+丨BC丨,则丨CD丨=丨BH丨=丨AB丨×sinα,即可求得四边形ABCD的周长.
解答 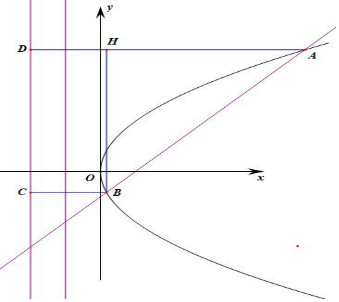 解:方法一:抛物线C:y2=4x的焦点是F(1,0),直线直线l1:y=x-1故抛物线的焦点,设A(x1,y1),B(x2,y2),
解:方法一:抛物线C:y2=4x的焦点是F(1,0),直线直线l1:y=x-1故抛物线的焦点,设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x-1}\end{array}\right.$,整理得:x2-6x+1=0,
x1+x2=6,
由丨AB丨=x1+x2+p=6+2+8,
由抛物线的定义可知:丨AD丨+丨BC丨=丨AB丨+2=10,
过B作BH⊥AD,
则由直线AB的倾斜角α=$\frac{π}{4}$,
则丨BH丨=丨AB丨×sinα=4$\sqrt{2}$,则丨CD丨=丨BH丨=4$\sqrt{2}$,
四边形ABCD的周长丨AB丨+丨AD丨+丨BC丨+丨CD丨=18+4$\sqrt{2}$,
故答案为:18+4$\sqrt{2}$.
方法二:抛物线C:y2=4x的焦点是F(1,0),直线直线l1:y=x-1故抛物线的焦点,由直线AB的倾斜角α=$\frac{π}{4}$,
由丨AB丨=$\frac{2p}{si{n}^{2}α}$=$\frac{4}{(\frac{\sqrt{2}}{2})^{2}}$=8,
由抛物线的定义可知:丨AD丨+丨BC丨=丨AB丨+2=10,
则丨BH丨=丨AB丨×sinα=4$\sqrt{2}$,则丨CD丨=丨BH丨=4$\sqrt{2}$,
四边形ABCD的周长丨AB丨+丨AD丨+丨BC丨+丨CD丨=18+4$\sqrt{2}$,
故答案为:18+4$\sqrt{2}$.
点评 本题考查直线与抛物线位置关系,考查抛物线的焦点弦公式,抛物线的定义,考查数形结合思想,属于中档题.

| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
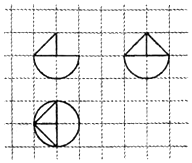
| A. | 3π+$\sqrt{3}$ | B. | 3π+$\sqrt{3}$+1 | C. | 5π+$\sqrt{3}$ | D. | 5π+$\sqrt{3}$+1 |
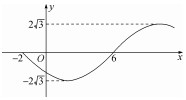 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数g(x)=Acos(φx+ω)图象的一个对称中心可能为( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |