题目内容
函数f(x)=
是奇函数,其中b为正整数,f(1)=2,且f(2)>2.
(1)求函数f(x)的解析式及定义域;
(2)证明函数f(x)在[
,1]上的单调性,并求出f(x)在该区f(x)在该区间上的值域.
| x2+a |
| bx+c |
(1)求函数f(x)的解析式及定义域;
(2)证明函数f(x)在[
| 1 |
| 2 |
考点:函数单调性的判断与证明,函数的定义域及其求法,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的综合应用
分析:(1)根据f(x)为奇函数可求出c=0,由b∈N*,及f(1)=2,f(2)>2能够求出a,b;
(2)求f′(x),判断f′(x)的符号,从而得到函数f(x)在[
,1]上单调递减,根据单调性即可f(x)在该区间上的值域.
(2)求f′(x),判断f′(x)的符号,从而得到函数f(x)在[
| 1 |
| 2 |
解答:
解:(1)∵f(x)是奇函数,∴f(-x)=
=-
,∴c=0;
f(1)=
=2,∴a=2b-1 ①;
f(2)=
>2 ②,将①带入②得
>2,∵b∈N*,∴b<
,∴b=1,a=1;
∴f(x)=
;
(2)f′(x)=
,∵x∈[
,1],∴f′(x)≤0,即f(x)在[
,1]上单调递减;
∴f(x)∈[f(1),f(
)]=[2,
],即函数f(x)的值域为[2,
].
| x2+a |
| -bx+c |
| x2+a |
| bx+c |
f(1)=
| 1+a |
| b |
f(2)=
| 4+a |
| 2b |
| 3+2b |
| 2b |
| 3 |
| 2 |
∴f(x)=
| x2+1 |
| x |
(2)f′(x)=
| x2-1 |
| x2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)∈[f(1),f(
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
点评:考查奇函数的定义,函数导数符号和函数单调性的关系,注意要正确求导.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c,若a2-b2=
bc,且sinC=2
sinB,则A等于( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
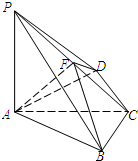 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.