题目内容

在△ABC中，若tanAtanB=1，则△ABC的形状是（　　）
A、等边三角形
B、等腰三角形
C、等腰直角三角形
D、直角三角形
考点：三角形的形状判断
专题：三角函数的求值
分析：tanAtanB=1⇒
sinAsinB-cosAcosB
cosAcosB
=0，从而可得cos（A+B）=0，于是可得答案．
解答： 解：在△ABC中，∵tanAtanB=1，
∴
sinAsinB-cosAcosB
cosAcosB
=0，
∴sinAsinB-cosAcosB=-cos（A+B）=0，
∴cos（π-C）=0，即cosC=0，C=90°，
∴△ABC为直角三角形，
故选：D．
点评：本题考查三角形的形状判断，考查两角和的余弦与诱导公式的应用，“切”化“弦”是关键，属于中档题．
练习册系列答案
相关题目
已知m，n为直线，a，b为平面，给出下列命题，其中的正确命题序号是
 

①
m⊥α
m⊥n
⇒n∥α  ②
m⊥β
n⊥β
⇒m∥n  ③
m⊥α
m⊥β
⇒α∥β  ④
m?α
n?β⇒m∥n
α∥β
．
甲、乙两人练习射击，命中目标的概率分别为
1
2
和
1
3
，甲、乙两人各射击一次，目标被命中的概率为（　　）
A、
2
3
B、
1
3
C、
1
6
D、
5
6
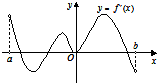函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值（　　）
A、2个B、1个C、3个D、4个
已知两个平面α，β，直线l⊥α，直线m?β，有下面四个命题：
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l⊥m⇒α∥β；④l∥m⇒α⊥β，其中正确命题有（　　）
A、①②B、①④C、②③D、①③
将函数f（x）=2sin（2x-θ）-3的图象F，向左平移
π
6
个单位，向上平移3个单位得到图象F′，若F′的一条对称轴是直线x=
π
4
，则θ的一个可能取值是（　　）
A、-
π
6
B、-
π
3
C、
π
2
D、
π
3
设函数f（x）=（x-1）2+n （x∈[-1，3]，n∈N*）的最小值为an，最大值为bn，记cn=bn2-anbn，则{cn}是（　　）
A、常数数列
B、公比不为1的等比数列
C、公差不为0的等差数列
D、非等差数列也非等比数列
设
.
z
为复数z的共轭复数，且
.
z
•i=1+2i，则z等于（　　）
A、2-iB、2+i
C、1+2iD、1-2i
已知Sn为等差数列{an}的前n项和，且满足a2+a2013=32，则log2
S2014
2014
=（　　）
A、6B、5C、4D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网