题目内容
甲、乙两人练习射击,命中目标的概率分别为
和
,甲、乙两人各射击一次,目标被命中的概率为( )
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:计算题,概率与统计
分析:对立事件的概率之和为1,相互独立事件的概率用乘法法则.
解答:
解:∵甲、乙两人各射击一次,目标没被命中的概率为(1-
)×(1-
)=
,
∴甲、乙两人各射击一次,目标被命中的概率为1-
=
.
故选A.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴甲、乙两人各射击一次,目标被命中的概率为1-
| 1 |
| 3 |
| 2 |
| 3 |
故选A.
点评:本题考查了概率的基本性质及相互独立事件同时发生的概率,属于基础题.

练习册系列答案
相关题目
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则对任意正整数n,下列式子成立的是( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(n+1)<f(-n)<f(n-1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(-n)<f(n-1)<f(n+1) |
| D、f(n+1)<f(n-1)<f(-n) |
已知函数f(x)=sin x+ln x,则f′(1)的值为( )
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
在△ABC中,若tanAtanB=1,则△ABC的形状是( )
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
函数y=2sinx,x∈[
,
]和y=2的图象围成了一个封闭图形,则此封闭图形的面积是( )
| π |
| 2 |
| 5π |
| 2 |
| A、4 | B、2π | C、4π | D、8π |
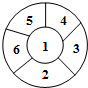 如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有
如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有