��Ŀ����
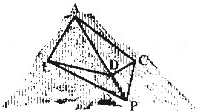 ij�ȼ�����2014���������»�Ϊ��������ɽ���˸�ɽ��ѩ����Ϊ����Ӧ��ͬ��Ⱥ����Ҫ����ɽ��A����ɽ�Ż�ѩ������P�����˻�ѩ����A-C-P�ͻ�ѩ��ϰ��A-E-P����ͼ������֪cos��ACP=һ
ij�ȼ�����2014���������»�Ϊ��������ɽ���˸�ɽ��ѩ����Ϊ����Ӧ��ͬ��Ⱥ����Ҫ����ɽ��A����ɽ�Ż�ѩ������P�����˻�ѩ����A-C-P�ͻ�ѩ��ϰ��A-E-P����ͼ������֪cos��ACP=һ
| ||
| 5 |
| 4 |
| 5 |
| 2 |
| 3 |
������CP�ij��ȣ�
��������C��E�����¹ʵĸ߷�����Ϊ��ʱ�����¹ʣ��ȼ����ƻ��ڹ�·AP����һ��D�������ӵ�
DC��DE����DP�ʱ������ʹ���ӵ�DC+DE��̣����Ϊ���ٰ��ף�
���㣺�������ε�ʵ��Ӧ��
ר�⣺�ۺ���,��������
���������������sin��PAC=sin����ACP+��APC��=
�����������Ҷ�����CP�ij��ȣ�
�����������Ҷ�������DE��DC�������䷽��������DC+DE��̣�
| ||
| 5 |
�����������Ҷ�������DE��DC�������䷽��������DC+DE��̣�
���
�⣺����cos��ACP=һ
��cos��APC=
��
��sin��ACP=
��sin��APC=
��
��sin��PAC=sin����ACP+��APC��=
��
��
=
��
��CP=5��������CP�ij���Ϊ5���ף�
������DP=x��x��[0��10]��
��EP=6��CP=5��cos��APC=
��cos��APE=
��
��DE=
=
��
DC=
=
��DE+DC=
+
=
+
��
���ҽ���x=4ʱ����DE+DC��min=3+2
��
| ||
| 5 |
| 4 |
| 5 |
��sin��ACP=
2
| ||
| 5 |
| 3 |
| 5 |
��sin��PAC=sin����ACP+��APC��=
| ||
| 5 |
��
| AP |
| sin��ACP |
| PC |
| sin��PAC |
��CP=5��������CP�ij���Ϊ5���ף�
������DP=x��x��[0��10]��
��EP=6��CP=5��cos��APC=
| 4 |
| 5 |
| 2 |
| 3 |
��DE=
| x2+36-2x•6•cos��APE |
| x2-8x+36 |
DC=
| x2+25-2x•5•cos��APC |
| x2-8x+25 |
��DE+DC=
| x2-8x+36 |
| x2-8x+25 |
| (x-4)2+20 |
| (x-4)2+9 |
���ҽ���x=4ʱ����DE+DC��min=3+2
| 5 |
���������⿼�����Ҷ��������Ҷ��������ã������䷽��������ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
�輯��M={x|x2��4}��N={x|x+1��0}����∁RM����N=��������
| A��{x|-1��x��2} |
| B��{x|x��2} |
| C��{x|-1��x��2} |
| D��{x|x��2} |
�ڡ�ABC�У�
=2
��
=
��
=
��
=
�������е�ʽ�������ǣ�������
| AD |
| DC |
| BA |
| a |
| BD |
| b |
| BC |
| c |
A��
| ||||||||||
B��
| ||||||||||
C��
| ||||||||||
D��
|
