题目内容
已知f(x)=lnx,g(x)=
-
.
(Ⅰ)当x≥1时,求f(x)-g(x)的最大值;
(Ⅱ)求证:
<
<
,?x>1恒成立;
(Ⅲ)求证:
+
<
<
+
(n≥2,n∈N).(参考数据:ln3≈1.1,ln5≈1.6)
| x |
| 1 | ||
|
(Ⅰ)当x≥1时,求f(x)-g(x)的最大值;
(Ⅱ)求证:
| x |
| x-1 |
| lnx |
| x+1 |
| 2 |
(Ⅲ)求证:
| n2 |
| 2 |
| 3n |
| 8 |
| n |
 |
| k=1 |
| 1 | ||
ln
|
| n2 |
| 2 |
| n |
| 2 |
考点:函数单调性的性质,函数单调性的判断与证明,函数的最值及其几何意义
专题:函数的性质及应用
分析:(Ⅰ)设F(x)=f(x)-g(x),x≥1,根据F′(x)≤0,可得F(x)在区间[1,+∞)内单调递减,从而求得F(x)的最大值.
(Ⅱ)由(Ⅰ)得,对?x≥1,都有
<
.设G(x)=(x+1)lnx-2(x-1),x>1,利用导数的符号可得G(x)在区间(1,+∞)内单调递增,故G(x)>G(1),化简可得
<
,原命题得证.
(Ⅲ)由(Ⅱ)得,x>1时,
<
<
恒成立.令
=x,k∈N*,可得
<
+
.当k≥2时,根据
>
>k-
,可得
>
+
(k-
)>
+
,从而命题得证.
(Ⅱ)由(Ⅰ)得,对?x≥1,都有
| x |
| x-1 | ||
|
| x-1 |
| lnx |
| x+1 |
| 2 |
(Ⅲ)由(Ⅱ)得,x>1时,
| ||
| x-1 |
| 1 |
| lnx |
| x+1 |
| 2(x-1) |
| 2k+1 |
| 2k-1 |
| n |
 |
| k=1 |
| 1 | ||
ln
|
| n2 |
| 2 |
| n |
| 2 |
| 1 | ||
ln(
|
| ||
| 2 |
| 1 |
| 8 |
| n |
 |
| k=1 |
| 1 | ||
ln
|
| 1 |
| ln3 |
| n |
 |
| k=2 |
| 1 |
| 8 |
| n2 |
| 2 |
| 3n |
| 8 |
解答:
解:(Ⅰ)设F(x)=f(x)-g(x)=lnx-(
-
),x≥1,
则F′(x)=
-
=-
≤0,
∴F(x)在区间[1,+∞)内单调递减,故F(x)的最大值为F(1)=0.
(Ⅱ)由(Ⅰ)得,对?x≥1,都有f(x)<g(x),即lnx<
-
=
.
∵x-1>0,lnx>0,∴
<
.
设G(x)=(x+1)lnx-2(x-1),x>1,则G′(x)=lnx+
-2=
.
设H(x)=xlnx-x+1,则H′(x)=lnx>0,
∴H(x)在区间(1,+∞)内单调递增,∴H(x)>H(1)=0,即G(x)>0.
∴G(x)在区间(1,+∞)内单调递增,∴G(x)>G(1)=0,即(x+1)lnx>2(x-1).
因为x-1>0,lnx>0,所以
<
,从而原命题得证.
(Ⅲ)由(Ⅱ)得,当x>1时,
<
<
恒成立.
令
=x,k∈N*,得
<
<k.
∴
<
k=
+
;
另一方面,当k≥2时,
>
>
=k-
,
∴
>
+
(k-
)>
+
-
=
+
,
从而命题得证.
| x |
| 1 | ||
|
则F′(x)=
| 1 |
| x |
| 1 | ||
2
|
(
| ||
2x
|
∴F(x)在区间[1,+∞)内单调递减,故F(x)的最大值为F(1)=0.
(Ⅱ)由(Ⅰ)得,对?x≥1,都有f(x)<g(x),即lnx<
| x |
| 1 | ||
|
| x-1 | ||
|
∵x-1>0,lnx>0,∴
| x |
| x-1 | ||
|
设G(x)=(x+1)lnx-2(x-1),x>1,则G′(x)=lnx+
| x+1 |
| x |
| xlnx-x+1 |
| x |
设H(x)=xlnx-x+1,则H′(x)=lnx>0,
∴H(x)在区间(1,+∞)内单调递增,∴H(x)>H(1)=0,即G(x)>0.
∴G(x)在区间(1,+∞)内单调递增,∴G(x)>G(1)=0,即(x+1)lnx>2(x-1).
因为x-1>0,lnx>0,所以
| x-1 |
| lnx |
| x+1 |
| 2 |
(Ⅲ)由(Ⅱ)得,当x>1时,
| ||
| x-1 |
| 1 |
| lnx |
| x+1 |
| 2(x-1) |
令
| 2k+1 |
| 2k-1 |
| ||
| 2 |
| 1 | ||
ln(
|
∴
| n |
 |
| k=1 |
| 1 | ||
ln
|
| n |
 |
| k=1 |
| n2 |
| 2 |
| n |
| 2 |
另一方面,当k≥2时,
| 1 | ||
ln(
|
| ||
| 2 |
| ||||
| 2 |
| 1 |
| 8 |
∴
| n |
 |
| k=1 |
| 1 | ||
ln
|
| 1 |
| ln3 |
| n |
 |
| k=2 |
| 1 |
| 8 |
| 7 |
| 8 |
| (n-1)(n+2) |
| 2 |
| n-1 |
| 8 |
| n2 |
| 2 |
| 3n |
| 8 |
从而命题得证.
点评:本题主要考查函数的单调性的判断和证明,利用函数的单调性求函数的最值,属于中档题.

练习册系列答案
相关题目
 为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )
为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )| A、10 | B、15 | C、30 | D、75 |
向边长分别为5,6,
的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为( )
| 13 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
 如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.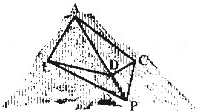 某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一
某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一