题目内容
设集合M={x|x2≥4}，N={x|x+1≥0}，则（∁RM）∩N=（ ）
| A、{x|-1≤x＜2} |
| B、{x|x＜2} |
| C、{x|-1＜x＜2} |
| D、{x|x≤2} |
考点：交、并、补集的混合运算
专题：集合
分析：分别求出M与N中不等式的解集，确定出M与N，根据全集R求出M的补集，找出M补集与N的交集即可．
解答：
解：由M中的不等式解得：x≤-2或x≥2，即M={x|x≤-2或x≥2}，
由N中的不等式解得：x≥-1，即N={x|x≥-1}，
∵全集为R，∴∁RM={x|-2＜x＜2}，
则（∁RM）∩N={x|-1≤x＜2}．
故选：A．
由N中的不等式解得：x≥-1，即N={x|x≥-1}，
∵全集为R，∴∁RM={x|-2＜x＜2}，
则（∁RM）∩N={x|-1≤x＜2}．
故选：A．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
设复数z满足（z+1）i=-3+2i（i为虚数单位），则z的实部是（ ）
| A、1 | B、2 | C、3 | D、4 |
双曲线
-
=1的离心率e=2，则双曲线的渐近线方程为（ ）
| y2 |
| 16 |
| x2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
取一根长度为4米的绳子，拉直后在任意位置剪断，那么剪得的两段都不少于1米的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
为监测幼儿身体发育状况，某幼儿园对“大班”的100名幼儿的体重做了测量，并根据所得数据画出了频率分布直方图，如图所示．则体重在[18，20]（单位kg）的幼儿人数为（ ）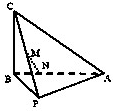
如图，在三棱锥C-PAB中，AB⊥BC，PB⊥BC，PA=PB=5，AB=6，BC=4，点M是PC的中点，点N在线段AB上，且MN⊥AB．
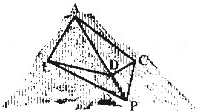某度假区以2014年索契冬奥会为契机，依山修建了高山滑雪场．为了适应不同人群的需要，从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P（如图）．已知cos∠ACP=一