题目内容
已知首项为正数的等差数列{an}中,a1a2=-2.则当a3取最大值时,数列{an}的公差d= .
考点:等差数列的性质
专题:等差数列与等比数列
分析:设公差为d,则由题意可得a1(a1+d)=-2,求得d=-
-a1,再根据a3=a1+2d=-(
+a1),利用基本不等式,求得当a3取最大值时,d的值.
| 2 |
| a1 |
| 4 |
| a1 |
解答:
解:首项为正数的等差数列{an}中,a1a2=-2,设公差为d,
则 a1(a1+d)=-2,∴d=-
-a1,
∴a3=a1+2d=-(
+a1)≤-2
=-4,当且仅当a1=2时,等号成立,
此时,d=-
-a1=-1-2=-3.
即当d=-3时,a3取最大值.
故答案为:-3.
则 a1(a1+d)=-2,∴d=-
| 2 |
| a1 |
∴a3=a1+2d=-(
| 4 |
| a1 |
| 4 |
此时,d=-
| 2 |
| a1 |
即当d=-3时,a3取最大值.
故答案为:-3.
点评:本题主要考查等差数列的定义和通项公式,基本不等式的应用,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
从[0,10]中任取一个数x,从[0,6]中任取一个数y,则使|x-5|+|y-3|≤4的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
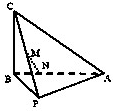 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.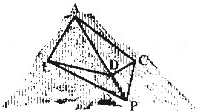 某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一
某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.