题目内容
已知函数f(x)=loga
,g(x)=1+loga(x-1),(a>0且a≠1),设f(x)和g(x)的定义域的公共部分为D,当[m,n]?D时,f(x)在[m,n](m<n)上的值域是[g(n),g(m)],求实数a的取值范围.
| x-3 |
| x+3 |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:由函数f(x)的解析式求得f(x)的定义域为(-∞,-3)∪(3,+∞).同理求得函数g(x)的定义域为(1,+∞),可得D=(3,+∞),根据f(x)在[m,n](m<n)上的值域是[g(n),g(m)],可得 g(x)在[m,n]上是减函数,故有0<a<1.
解答:
解:∵函数f(x)=loga
,∴
>0,解得x>3,或x<-3,
故函数f(x)的定义域为(-∞,-3)∪(3,+∞).
∵g(x)=1+loga(x-1),(a>0且a≠1),
∴x>1,故函数g(x)的定义域为(1,+∞).
设f(x)和g(x)的定义域的公共部分为D,则D=(3,+∞),
∵当[m,n]?D时,f(x)在[m,n](m<n)上的值域是[g(n),g(m)],
∴g(x)在[m,n]上是减函数,故有0<a<1.
即实数a的取值范围为(0,1).
| x-3 |
| x+3 |
| x-3 |
| x+3 |
故函数f(x)的定义域为(-∞,-3)∪(3,+∞).
∵g(x)=1+loga(x-1),(a>0且a≠1),
∴x>1,故函数g(x)的定义域为(1,+∞).
设f(x)和g(x)的定义域的公共部分为D,则D=(3,+∞),
∵当[m,n]?D时,f(x)在[m,n](m<n)上的值域是[g(n),g(m)],
∴g(x)在[m,n]上是减函数,故有0<a<1.
即实数a的取值范围为(0,1).
点评:本题主要考查对数函数的图象和性质综合应用,属于中档题.

练习册系列答案
相关题目
若集合A={1,m2},集合B={3,9},则“m=3”是“A∩B={9}”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
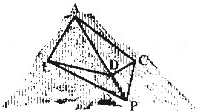 某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一
某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.