题目内容
已知曲线C的方程为:ax2+ay2-2a2x-4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=-2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=-2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)把方程化为圆的标准方程,可得结论;
(2)求出A,B的坐标,即可得出△AOB的面积S为定值;
(3)由圆C过坐标原点,且|OM|=|ON|,可得圆心(a,
)在MN的垂直平分线上,从而求出a,再判断a=-2不合题意即可.
(2)求出A,B的坐标,即可得出△AOB的面积S为定值;
(3)由圆C过坐标原点,且|OM|=|ON|,可得圆心(a,
| 2 |
| a |
解答:
解:(1)将曲线C的方程化为(x-a)2+(y-
)2=a2+
--(2分)
可知曲线C是以点(a,
)为圆心,以
为半径的圆.-----------------------------(4分)
(2)△AOB的面积S为定值.-------------------------------------------(5分)
证明如下:
在曲线C的方程中令y=0得ax(x-2a)=0,得点A(2a,0),---------------------------(6分)
在曲线C的方程中令x=0得y(ay-4)=0,得点B(0,
),--------------------------(7分)
∴S=
|OA||OB|=
|2a||
|=4(为定值).----------------------------------------(9分)
(3)∵圆C过坐标原点,且|OM|=|ON|,
∴圆心(a,
)在MN的垂直平分线上,∴
=
,∴a=±2,--------------------(11分)
当a=-2时,圆心坐标为(-2,-1),圆的半径为
,
圆心到直线l:y=-2x+4的距离d=
=
>
,
直线l与圆C相离,不合题意舍去,--------------------------------------(13分)
∴a=2,这时曲线C的方程为x2+y2-4x-2y=0.-----------------------------------(14分)
| 2 |
| a |
| 4 |
| a2 |
可知曲线C是以点(a,
| 2 |
| a |
a2+
|
(2)△AOB的面积S为定值.-------------------------------------------(5分)
证明如下:
在曲线C的方程中令y=0得ax(x-2a)=0,得点A(2a,0),---------------------------(6分)
在曲线C的方程中令x=0得y(ay-4)=0,得点B(0,
| 4 |
| a |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| a |
(3)∵圆C过坐标原点,且|OM|=|ON|,
∴圆心(a,
| 2 |
| a |
| 2 |
| a2 |
| 1 |
| 2 |
当a=-2时,圆心坐标为(-2,-1),圆的半径为
| 5 |
圆心到直线l:y=-2x+4的距离d=
| |-4-1-4| | ||
|
| 9 | ||
|
| 5 |
直线l与圆C相离,不合题意舍去,--------------------------------------(13分)
∴a=2,这时曲线C的方程为x2+y2-4x-2y=0.-----------------------------------(14分)
点评:本题考查圆的方程,考查直线与圆的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
设复数z满足(z+1)i=-3+2i(i为虚数单位),则z的实部是( )
| A、1 | B、2 | C、3 | D、4 |
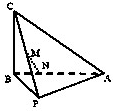 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB. 如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.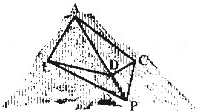 某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一
某度假区以2014年索契冬奥会为契机,依山修建了高山滑雪场.为了适应不同人群的需要,从山上A处到山脚滑雪服务区P处修建了滑雪赛道A-C-P和滑雪练习道A-E-P(如图).已知cos∠ACP=一