题目内容
8．若等比数列{an}的前n项和Sn=a+（$\frac{1}{2}$）n-2，则a=-4．分析 利用${a}_{n}=\left\{\begin{array}{l}{{S}_{1}，n=1}\\{{S}_{n}-{S}_{n-1}，n≥2}\end{array}\right.$，求出a1，a2，a3，由等比数列中，${{a}_{2}}^{2}={a}_{1}{a}_{3}$，能求出a．
解答 解：∵等比数列{an}的前n项和Sn=a+（$\frac{1}{2}$）n-2，
∴a1=S1=a+2，
a2=S2-S1=（a+1）-（a+2）=-1，
a3=S3-S2=（a+$\frac{1}{2}$）-（a+1）=-$\frac{1}{2}$，
∵等比数列中，${{a}_{2}}^{2}={a}_{1}{a}_{3}$，
∴1=-$\frac{1}{2}（a+2）$，
解得a=-4．
故答案为：-4．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点（2，1）在“右”区域内，则双曲线离心率e的取值范围是（ ）
| A． | $（{1，\frac{{\sqrt{5}}}{2}}）$ | B． | $（{\frac{{\sqrt{5}}}{2}，+∞}）$ | C． | $（{1，\frac{5}{4}}）$ | D． | $（{\frac{5}{4}，+∞}）$ |
19．已知i为虚数单位，复数z满足$\overline z（1+i）=i$，则z=（ ）
| A． | 1+i | B． | 1-i | C． | $\frac{1}{2}+\frac{1}{2}i$ | D． | $\frac{1}{2}-\frac{1}{2}i$ |
13．设α，β，γ表示平面，l表示直线，则下列命题中，错误的是（ ）
| A． | 如果α⊥β，那么α内一定存在直线平行于β | |
| B． | 如果α⊥γ，β⊥γ，α∩β=l，那么l⊥γ | |
| C． | 如果α不垂直于β，那么α内一定不存在直线垂直于β | |
| D． | 如果α⊥β，那么α内所有直线都垂直于β |
20．
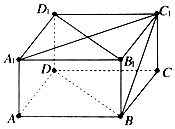如图，已知长方体ABCD-A1B1C1D1中，AB=BC=4，CC1=2，则直线BC1和平面DBB1D1所成角的正弦值等于（ ）
如图，已知长方体ABCD-A1B1C1D1中，AB=BC=4，CC1=2，则直线BC1和平面DBB1D1所成角的正弦值等于（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\frac{\sqrt{10}}{5}$ | D． | $\frac{\sqrt{10}}{10}$ |
17．若sin（θ+3π）=$\frac{4}{5}$，tan（θ-π）＞0，则cosθ=（ ）
| A． | $\frac{3}{5}$ | B． | $-\frac{4}{5}$ | C． | $-\frac{3}{5}$ | D． | $\frac{4}{5}$ |