题目内容
20.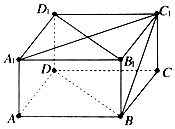 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{10}$ |
分析 要求线面角,先寻找斜线在平面上的射影,因此,要寻找平面的垂线,利用已知条件可得.
解答  解:由题意,连接A1C1,交B1D1于点O,
解:由题意,连接A1C1,交B1D1于点O,
∵长方体ABCD-A1B1C1D1中,AB=BC=4,
∴C1O⊥B1D1
∴C1O⊥平面DBB1D1
在Rt△BOC1中,C1O=2$\sqrt{2}$,BC1=2$\sqrt{5}$,
∴直线BC1和平面DBB1D1所成角的正弦值为$\frac{\sqrt{10}}{5}$,
故选:C.
点评 本题的考点是直线与平面所成的角,主要考查线面角,关键是寻找线面角,通常寻找斜线在平面上的射影.

练习册系列答案
相关题目
11.若复数(a2+i)(1+ai)(a∈R)是实数,则实数a的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
15.已知点P是双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,F1,F2分别是双曲线的左、右焦点,I为△PF1F2的内心,若S${\;}_{△IP{F}_{1}}$=S${\;}_{△IP{F}_{2}}$$+\frac{1}{2}$S${\;}_{△I{F}_{1}{F}_{2}}$成立,则双曲线的离心率为( )
| A. | 4 | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{5}{3}$ |
5.下列语句可以是赋值语句的是( )
| A. | S=a+1 | B. | a+1=S | C. | S-1=a | D. | S-a=1 |
9.将函数y=sin2x的图象向左平移φ(φ>0)个单位,得到的图象恰好关于直线x=$\frac{π}{6}$对称,则φ的最小值是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
4.已知M、N是焦点为F的抛物线y2=4x上两个不同点,且线段MN的中点A的横坐标是3,直线MN与x轴交于点B,则点B的横坐标的取值范围是( )
| A. | (-3,3] | B. | (-∞,3] | C. | (-6,-3] | D. | (-6,3) |