题目内容
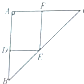 如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为
如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为考点:棱柱、棱锥、棱台的体积
专题:函数的性质及应用,导数的概念及应用,空间位置关系与距离
分析:由已知易得BD即为棱锥B-ADEF的高,此时底面ADEF为矩形,AD=2-x,DE=x,表示出棱锥B-ADEF的体积,利用导数法,可得棱锥B-ADEF的体积最大时,BD的长.
解答:
解:设BD的长为x时,棱锥B-ADEF的体积最大,
∵等腰直角△ABC中,AB=2,DE∥AC,EF∥AB,
∴BD即为棱锥B-ADEF的高,
此时底面ADEF为矩形,AD=2-x,DE=x,
故棱锥B-ADEF的体积V=
×BD×AD×DF=
(2-x)•x•x=-
x3+
x2,
则V′=-x2+
x,
当x<
时,V′>0,此时函数为增函数,当
<x<2时,V′<0,此时函数为减函数,
故当BD=
时,棱锥B-ADEF的体积最大,
故答案为:
∵等腰直角△ABC中,AB=2,DE∥AC,EF∥AB,
∴BD即为棱锥B-ADEF的高,
此时底面ADEF为矩形,AD=2-x,DE=x,
故棱锥B-ADEF的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
则V′=-x2+
| 4 |
| 3 |
当x<
| 4 |
| 3 |
| 4 |
| 3 |
故当BD=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查的知识点是棱锥的体积,导数法研究函数的最值,难度中档.

练习册系列答案
相关题目
已知f(x)=sin(ωx+
),(ω>0)的图象与y=1的图象的两相邻交点间的距离为π,
要得到y=f(x)的图象,只须把y=sinωx的图象( )
| π |
| 3 |
要得到y=f(x)的图象,只须把y=sinωx的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
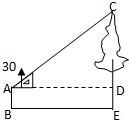 如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )A、(
| ||||||
B、(5
| ||||||
C、
| ||||||
| D、4m |
已知
,
均为单位向量,它们的夹角为60°,那么|
+2
|等于( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
 如图,在矩形ABCD中,AB=2,AD=
如图,在矩形ABCD中,AB=2,AD=