题目内容
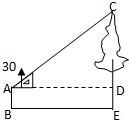如图，小明利用有一个锐角是30°的三角板测量一棵树的高度，已知他与树之间的水平距离BE为5m，AB为1.5m（即小明的眼睛距地面的距离），那么这棵树高是（ ）A、（
| ||||||
B、（5
| ||||||
C、
| ||||||
| D、4m |
考点：在实际问题中建立三角函数模型
专题：应用题,解三角形
分析：先根据题意得出AD的长，在Rt△ACD中利用锐角三角函数的定义求出CD的长，由CE=CD+DE即可得出结论．
解答：
解：∵AB⊥BE，DE⊥BE，AD∥BE，
∴四边形ABED是矩形，
∵BE=5m，AB=1.5m，
∴AD=BE=5m，DE=AB=1.5m，
在Rt△ACD中，
∵∠CAD=30°，AD=5m，
∴CD=AD•tan30°=5×
=
，
∴CE=CD+DE=
+
（m）．
故选：A．
∴四边形ABED是矩形，
∵BE=5m，AB=1.5m，
∴AD=BE=5m，DE=AB=1.5m，
在Rt△ACD中，
∵∠CAD=30°，AD=5m，
∴CD=AD•tan30°=5×
| ||
| 3 |
5
| ||
| 3 |
∴CE=CD+DE=
5
| ||
| 3 |
| 3 |
| 2 |
故选：A．
点评：本题考查的是解直角三角形在实际生活中的应用，熟知锐角三角函数的定义是解答此题的关键，属于基本知识的考查．
练习册系列答案
相关题目
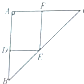如图，等腰直角△ABC中，AB=2，D、E、F分别在边AB、BC、CA上，且DE∥AC，EF∥AB，现沿DE折叠，使平面BDE⊥平面ADEF，若此时棱锥B-ADEF的体积最大，则BD的长为若直线（1+a）x+y+1=0与圆x2+y2-2x=0相切，则a的值为（ ）
| A、-1，1 | B、-2，2 |
| C、1 | D、-1 |
曲线y=x3与直线y=x所围成图形的面积为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
