题目内容
已知函数f(x)=lg(
+n)的图象关于原点对称(m、n∈R,m>0),求m,n.
| mx |
| x+1 |
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:由题意,f(-x)+f(x)=0恒成立,即
=0,从而可得
从而求m,n.
| [(m+n)2-1]x2+1-n2 |
| x2-1 |
|
解答:
解:∵函数f(x)=lg(
+n)的图象关于原点对称,
∴f(-x)+f(x)=0,
∴lg(
+n)+lg(
+n)=0,
∴(
+n)•(
+n)=1,
∴
=0,
∴
解得,n=-1,m=2.
| mx |
| x+1 |
∴f(-x)+f(x)=0,
∴lg(
| -mx |
| -x+1 |
| mx |
| x+1 |
∴(
| -mx |
| -x+1 |
| mx |
| x+1 |
∴
| [(m+n)2-1]x2+1-n2 |
| x2-1 |
∴
|
解得,n=-1,m=2.
点评:本题考查了函数的奇偶性的应用,属于基础题.

练习册系列答案
相关题目
曲线y=x3与直线y=x所围成图形的面积为( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
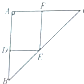 如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为
如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为