题目内容

求证：tan2α-sin2α=tan2α•sin2α
考点：三角函数恒等式的证明
专题：三角函数的求值
分析：直接利用切化弦，证明三角恒等式即可．
解答： 证明：左边=tan2α-sin2α=
sin2α
cos2α
-sin2α=sin2α[
1-cos2α
cos2α
]=sin2α•
sin2α
cos2α
=tan2α•sin2α=右边．
等式成立．
点评：本题考查三角恒等式的证明，基本知识的考查．
练习册系列答案
相关题目
已知椭圆的焦点为F（1，0），离心率e=
1
2
，过点F的直线l交椭圆于M、N两点，MN的中垂线交y轴于点P，求点P纵坐标的取值范围．
已知函数y=2tan（2x+φ）是奇函数，则φ=
 
．
已知函数f（x）=loga（x2-ax+3），若函数f（x）的值域为R，求实数a的取值范围．
在△ABC中，若a=2，b=1，∠B=45°，则此三角形有
 
个解．
已知函数f（x）=
2x+a
2x+1
（a∈R），
（1）确定实数a的值，使f（x）为奇函数；
（2）在（1）的基础上，判断f（x）的单调性并证明；
（3）在（1）的基础上，求f（x）的值域．
一物体相对于某一固定位置的位移y（cm）和时间t（s）之间的一组对应值如表所示，
t（s）00.10.20.30.40.50.60.70.8
Y（cm）-4.0-2.80.02.84.02.80.0-2.8-4.0
则可近似地描述该物体的位移y和时间t之间关系的三角函数为
 
．
一质点运动方程S（t）=asint+bcost（a＞0），若速度v（t）最大值为
6
，且对任意的t0∈R，在t=t0与t=
π
2
-t0时速度相同，求a，b的值．
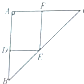如图，等腰直角△ABC中，AB=2，D、E、F分别在边AB、BC、CA上，且DE∥AC，EF∥AB，现沿DE折叠，使平面BDE⊥平面ADEF，若此时棱锥B-ADEF的体积最大，则BD的长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网