题目内容
设函数f(x)=x2+bx-alnx,
(Ⅰ) 若x=2是函数f(x)的极值点,1是函数f(x)的一个零点,求函数f(x)的解析式;
(Ⅱ) 若对任意b∈[-2,-1],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
(Ⅰ) 若x=2是函数f(x)的极值点,1是函数f(x)的一个零点,求函数f(x)的解析式;
(Ⅱ) 若对任意b∈[-2,-1],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求导得到f′(x)=2x-
+b,由,f(1)=1+b=0,得到a与b的值,继而求出函数的解析式,
(Ⅱ)令g(b)=xb+x2-alnx,b∈[-2,-1],问题转化为在x∈(1,e)上g(b)max=g(-1)<0有解即可,亦即只需存在x0∈(1,e)使得x2-x-alnx<0即可,连续利用导函数,然后分别对1-a≥0,1-a<0,看是否存在x0∈(1,e)使得h(x0)<h(1)=0,进而得到结论.
| a |
| x |
(Ⅱ)令g(b)=xb+x2-alnx,b∈[-2,-1],问题转化为在x∈(1,e)上g(b)max=g(-1)<0有解即可,亦即只需存在x0∈(1,e)使得x2-x-alnx<0即可,连续利用导函数,然后分别对1-a≥0,1-a<0,看是否存在x0∈(1,e)使得h(x0)<h(1)=0,进而得到结论.
解答:
解:(Ⅰ)f′(x)=2x-
+b,
∵x=2是函数f(x)的极值点,
∴f′(2)=4-
+b=0.
∵1是函数f(x)的零点,得f(1)=1+b=0,
由
,
解得a=6,b=-1.
∴f(x)=x2-x-6lnx,
(Ⅱ)令g(b)=xb+x2-alnx,b∈[-2,-1],则g(b)为关于b的一次函数且为增函数,
根据题意,对任意b∈[-2,-1],都存在x∈(1,e)(e 为自然对数的底数),使得f(x)<0成立,
则在x∈(1,e)上g(b)max=g(-1)=-x+x2-alnx<0,有解,
令h(x)=x2-x-alnx,只需存在x0∈(1,e)使得h(x0)<0即可,
由于h′(x)=2x-1-
,
令φ(x)=2x2-x-a,x∈(1,e),φ'(x)=4x-1>0,
∴φ(x)在(1,e)上单调递增,φ(x)>φ(1)=1-a,
①当1-a≥0,即a≤1时,φ(x)>0,即h′(x)>0,h(x)在(1,e)上单调递增,∴h(x)>h(1)=0,不符合题意.
②当1-a<0,即a>1时,φ(1)=1-a<0,φ(e)=2e2-e-a
若a≥2e2-e>1,则φ(e)<0,所以在(1,e)上φ(x)<0恒成立,即h′(x)<0恒成立,∴h(x)在(1,e)上单调递减,
∴存在x0∈(1,e)使得h(x0)<h(1)=0,符合题意.
若2e2-e>a>1,则φ(e)>0,∴在(1,e)上一定存在实数m,使得φ(m)=0,
∴在(1,m)上φ(x)<0恒成立,即h′(x)<0恒成立,∴h(x)在(1,e)上单调递减,
∴存在x0∈(1,e)使得h(x0)<h(1)=0,符合题意.
综上所述,当a>1时,对任意b∈[-2,-1],都存在x∈(1,e)(e 为自然对数的底数),使得f(x)<0成立.
| a |
| x |
∵x=2是函数f(x)的极值点,
∴f′(2)=4-
| a |
| 2 |
∵1是函数f(x)的零点,得f(1)=1+b=0,
由
|
解得a=6,b=-1.
∴f(x)=x2-x-6lnx,
(Ⅱ)令g(b)=xb+x2-alnx,b∈[-2,-1],则g(b)为关于b的一次函数且为增函数,
根据题意,对任意b∈[-2,-1],都存在x∈(1,e)(e 为自然对数的底数),使得f(x)<0成立,
则在x∈(1,e)上g(b)max=g(-1)=-x+x2-alnx<0,有解,
令h(x)=x2-x-alnx,只需存在x0∈(1,e)使得h(x0)<0即可,
由于h′(x)=2x-1-
| a |
| x |
令φ(x)=2x2-x-a,x∈(1,e),φ'(x)=4x-1>0,
∴φ(x)在(1,e)上单调递增,φ(x)>φ(1)=1-a,
①当1-a≥0,即a≤1时,φ(x)>0,即h′(x)>0,h(x)在(1,e)上单调递增,∴h(x)>h(1)=0,不符合题意.
②当1-a<0,即a>1时,φ(1)=1-a<0,φ(e)=2e2-e-a
若a≥2e2-e>1,则φ(e)<0,所以在(1,e)上φ(x)<0恒成立,即h′(x)<0恒成立,∴h(x)在(1,e)上单调递减,
∴存在x0∈(1,e)使得h(x0)<h(1)=0,符合题意.
若2e2-e>a>1,则φ(e)>0,∴在(1,e)上一定存在实数m,使得φ(m)=0,
∴在(1,m)上φ(x)<0恒成立,即h′(x)<0恒成立,∴h(x)在(1,e)上单调递减,
∴存在x0∈(1,e)使得h(x0)<h(1)=0,符合题意.
综上所述,当a>1时,对任意b∈[-2,-1],都存在x∈(1,e)(e 为自然对数的底数),使得f(x)<0成立.
点评:本题考查利用导数求函数性质的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答

练习册系列答案
相关题目
已知方程
x2+
x+
=0,其中
,
,
是非零向量,且
,
不共线,则该方程( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、至多有一个解 |
| B、至少有一个解 |
| C、至多有两个解 |
| D、可能有无数多个解 |
若直线(1+a)x+y+1=0与圆x2+y2-2x=0相切,则a的值为( )
| A、-1,1 | B、-2,2 |
| C、1 | D、-1 |
曲线y=x3与直线y=x所围成图形的面积为( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
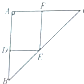 如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为
如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示(如图),则该赛季发挥更稳定的运动员是
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示(如图),则该赛季发挥更稳定的运动员是