题目内容
已知f(x)=sin(ωx+
),(ω>0)的图象与y=1的图象的两相邻交点间的距离为π,
要得到y=f(x)的图象,只须把y=sinωx的图象( )
| π |
| 3 |
要得到y=f(x)的图象,只须把y=sinωx的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:首项根据函数的图象与y=1的图象的两相邻交点间的距离为π,求出解析式,进一步根据图象的平移求出结果.
解答:
解:已知f(x)=sin(ωx+
),(ω>0)的图象与y=1的图象的两相邻交点间的距离为π.
则:T=π=
所以:ω=2
要得到y=f(x)=sin(2x+
)的图象,只需将y=sin2x的图象向左平移
各单位即可.
故选:A
| π |
| 3 |
则:T=π=
| 2π |
| ω |
所以:ω=2
要得到y=f(x)=sin(2x+
| π |
| 3 |
| π |
| 6 |
故选:A
点评:本题考查的知识要点:函数图象的平移变换问题,函数的周期的应用,属于基础题型.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知变量x,y满足约束条件
,则目标函数z=y-2x的最小值为( )
|
| A、-5 | B、-4 | C、-3 | D、-2 |
若直线(1+a)x+y+1=0与圆x2+y2-2x=0相切,则a的值为( )
| A、-1,1 | B、-2,2 |
| C、1 | D、-1 |
点P(x0,y0)在圆x2+y2=1外,则直线x0x+y0y=1与此圆的位置关系是( )
| A、相交 | B、相切 | C、相离 | D、不确定 |
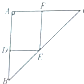 如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为
如图,等腰直角△ABC中,AB=2,D、E、F分别在边AB、BC、CA上,且DE∥AC,EF∥AB,现沿DE折叠,使平面BDE⊥平面ADEF,若此时棱锥B-ADEF的体积最大,则BD的长为