题目内容
已知首项a1=1各项都是正数的数列{an}(n∈N*),使目标函数z=3x+2y在约束条件
下最大值为2(an+1)2.
(1)求an与an+1的关系;
(2)证明:bn=
是等比数列;
(3)证明:
≤a1+a2+…+an≤
.
|
(1)求an与an+1的关系;
(2)证明:bn=
| 2an-1 |
| an+3 |
(3)证明:
| n+1 |
| 2 |
| n+2 |
| 2 |
考点:数列与不等式的综合,等比关系的确定
专题:等差数列与等比数列
分析:(1)画出平面区域,由Z的几何意义得出Z的最大值,即可求得结论;
(2)利用等比数列的定义证明即可;
(3)利用放缩法证明.
(2)利用等比数列的定义证明即可;
(3)利用放缩法证明.
解答:
解:(1)∵
∴画出其表示的平面区域如图:
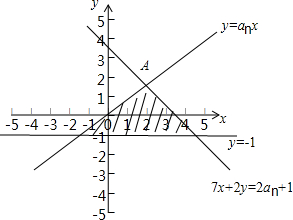
∴z=3x+2y即y=-
x+
过点A时Z有最大值,
由
解得A(
,
),
∴3×
+2×
=2(an+1)2.
∴an+1=
.
(2)bn=
,
∴bn+1=
=
=
•
=
bn,
又b1=
=
,
∴{bn}是首项为
,公比为
的等比数列.
(3)由(2)得bn=
×(
)n-1=
>0,
∴
=bn,解得an=
-3>
-3=
,
∴a1+a2+…+an≥a1+
+…+
=1+
=
,
又an=
-3=
=
+
=
+
≤
+
,
∴a1+a2+…+an≤
+
=
+1-
<
+1=
,
∴
≤a1+a2+…+an≤
.
|
∴画出其表示的平面区域如图:

∴z=3x+2y即y=-
| 3 |
| 2 |
| z |
| 2 |
由
|
| 2an+1 |
| 7+2an |
| 2anan+1 |
| 2an+7 |
∴3×
| 2an+1 |
| 7+2an |
| 2anan+1 |
| 2an+7 |
∴an+1=
| 2an+3 |
| 2an+7 |
(2)bn=
| 2an-1 |
| an+3 |
∴bn+1=
| 2an+1-1 |
| an+1+3 |
2•
| ||
|
| 1 |
| 8 |
| 2an-1 |
| an+3 |
| 1 |
| 8 |
又b1=
| 2×1-1 |
| 1+3 |
| 1 |
| 4 |
∴{bn}是首项为
| 1 |
| 4 |
| 1 |
| 8 |
(3)由(2)得bn=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 23n-1 |
∴
| 2an-1 |
| an+3 |
| 7 |
| 2-bn |
| 7 |
| 2 |
| 1 |
| 2 |
∴a1+a2+…+an≥a1+
| 1 |
| 2 |
| 1 |
| 2 |
| n-1 |
| 2 |
| n+1 |
| 2 |
又an=
| 7 |
| 2-bn |
| 1+3bn |
| 2-bn |
| 1 |
| 2 |
| ||
| 2-bn |
| 1 |
| 2 |
| 7 |
| 23n+1-2 |
| 1 |
| 2 |
| 1 |
| 2n |
∴a1+a2+…+an≤
| n |
| 2 |
| ||||
1-
|
| n |
| 2 |
| 1 |
| 2n |
| n |
| 2 |
| n+2 |
| 2 |
∴
| n+1 |
| 2 |
| n+2 |
| 2 |
点评:本题主要考查平面区域的画法及目标函数最值的求法,考查等比数列的定义及不等式的证明,考查学生放缩法的运用及运算求解能力,属于难题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
“a<-4”是函数f(x)=ax+3在[-1,1]上存在零点的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
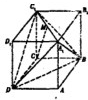 如图,在长方体ABCD-A1B1C1D1中,AB=
如图,在长方体ABCD-A1B1C1D1中,AB=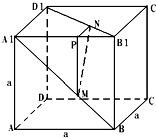 在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若
在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若
 如图是一个边长为1的正方形及其内切圆,现随机地向该正方形内投一粒黄豆(视为一点),则黄豆落入圆内的概率为
如图是一个边长为1的正方形及其内切圆,现随机地向该正方形内投一粒黄豆(视为一点),则黄豆落入圆内的概率为